准备搞明白泛函
无人机的动力学系统
- 运动轨迹方程与E-L方程
- 高阶E-L方程
- For $J[y(x)] = \int_{x_0}^{x_1}F(x, \dot x, \ddot x, \dotsc, x^{(n)})dx$
- 这里的$\dot x$为x的一阶导数,即速度,由于在力学领域,经常使用$\dot x, \ddot x$的形式描述高阶导数(牛顿导数记号),这里也一并改为此种写法
- E-L : $\frac{\partial F}{\partial x} - \frac{d}{dt}(\frac{\partial F}{\partial \dot x}) + \frac{d^2}{dt^2}(\frac{\partial F}{\partial \ddot x}) - \frac{d^3}{dt^3}(\frac{\partial F}{\partial x^{(3)}}) + \dotsc +(-1)^n \frac{d^n}{dt^n}(\frac{\partial F}{\partial x^{(n)}})= 0$
- 计算例子
- 求解从时间$0$到时间$t$, 速度的平方最小的函数, 即,一阶动力学问题
- 求解从时间$0$到时间$t$, 加加速度的平方最小的函数, 即,三阶动力学问题
- $J[x(t)] = \int_{0}^{T}(x^{(3)})^2dt$
- 此时的E-L方程
- 求解参数
- 边界(Boundary condition)
-
$$
\begin{cases}
[x, \dot x, \ddot x]\big |_{t=0} &= [a, 0, 0]&\text{假定初始速度为0,初始加速度为0,初始位置为a}\\
[x, \dot x, \ddot x]\big |_{t=T} &= [b, 0, 0]&\text{假定终止速度为0,终止加速度为0,终止位置为b}
\end{cases}
$$
- 列出求解矩阵
- 解出$c_0 ~ c_5$即可
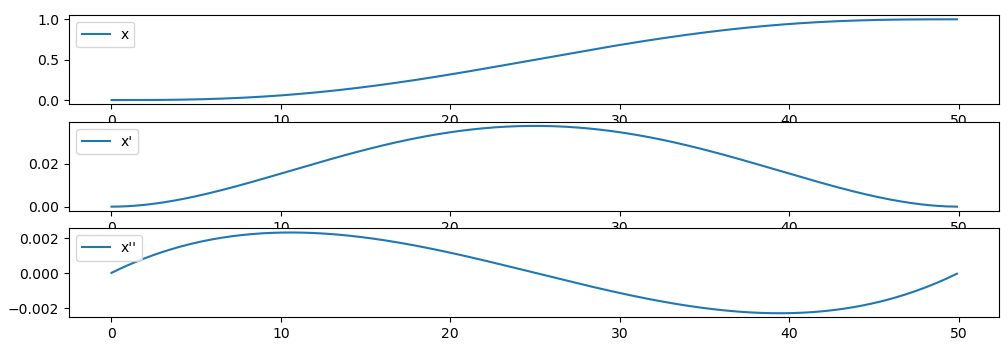
- 得到的位置,速度,加速度曲线如下(a=0, b=1, T=50)
- 多维E-L方程
- For $J[x(t), y(t)] = \int_0^TF(t, x, y, \dot x, \dot y)dt$
- E-L:
$\begin{aligned}
\frac{\partial F}{\partial x} - \frac{d}{dt}(\frac{\partial F}{\partial \dot x}) &= 0\\
\frac{\partial F}{\partial y} - \frac{d}{dt}(\frac{\partial F}{\partial \dot y}) &= 0
\end{aligned}$
- 使用例子
- 多段轨迹[增加约束条件]
- 使物体依次通过m个点,但由于运动时无法忽略惯性作用,因此我们需要增加速度约束
- For
$\begin{aligned}
t&=\begin{bmatrix}
t_0& t_1&\dotsc t_m
\end{bmatrix}^T&\\
x&=\begin{bmatrix}
x_0& x_1&\dotsc x_m
\end{bmatrix}^T&
\end{aligned}$
- $J[x(t)] = [\int_{t_0}^{t_1}(\ddot x^2)dx + \int_{t_1}^{t_2}(\ddot x^2)dx + \dotsc +\int_{t_{m-1}}^{t_m}(\ddot x^2)dx]$
- 分段求解,得到
$\begin{aligned}
x(t) = \begin{cases}
x_1(t) &= c_{10}t^3 + c_{11}t^2 + c_{12}t + c_{13}&t_0\le t\le t_1\\
x_2(t) &= c_{20}t^3 + c_{21}t^2 + c_{22}t + c_{23}&t_1\le t\le t_2\\
\dotsc\\
x_m(t) &= c_{m0}t^3 + c_{m1}t^2 + c_{m2}t + c_{m3}&t_0\le t\le t_m\\
\end{cases}
\end{aligned}$
- 为了求解$4m$个变量$c_{ij}$,我们需要$4m$个方程[约束]来进行确定
- 有位置方程
- $x_n(t_{n-1}) = x_{n-1}$ 前一个$x$是方程,后一个$x$是值, 共$m$个
- $x_n(t_n) = x_n$, 共$m$个
- 有速度方程[通过某一点,速度不变]
- $\dot x_n(t_n) = \dot x_{n+1}(t_n)$ 共$m-1$个
- $\dot x_1(t_0) = 0$ \ 终点停止
- 有加速度方程[加速度连续,不存在阶跃的情况]
- $\ddot x_n(t_n) = \ddot x_{n+1}(t_n)$ 共$m-1$个
- $\dot x_1(t_m) = 0$ \ 终点停止
- 共4m个方程组
- 利用以上方程组即可求解