Coordinate System in Dynamic
准备搞明白泛函
无人机的动力学系统
- 动力系统
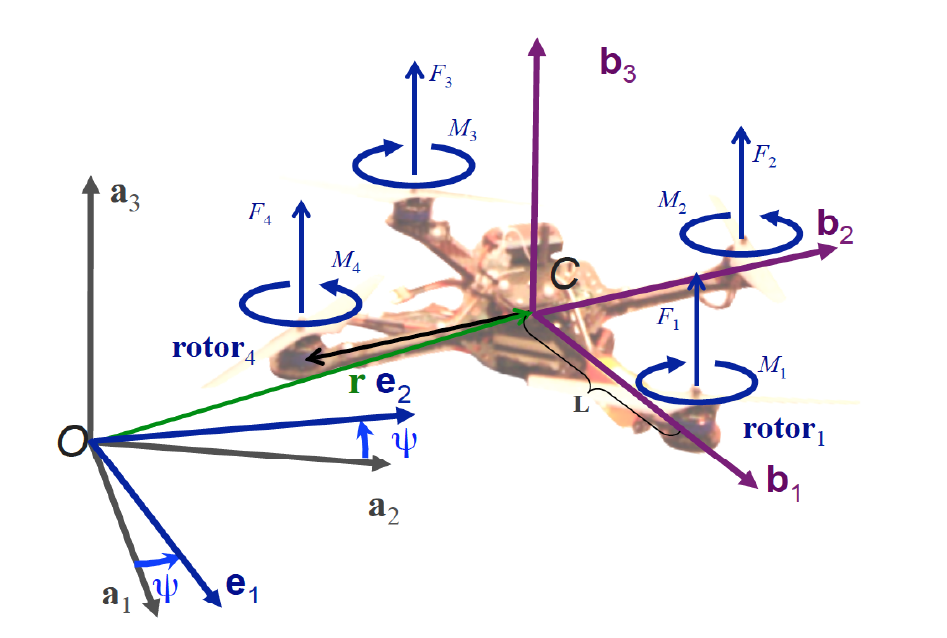
- 惯性系[inertial frame]$\mathbf{A}$
- 3个转轴$a_1, a_2, a_3$
- 原点$O$
- 随体系[body frame]或固连系[body-fixed frame]或体坐标系[body coordinate]$\mathbf{B}$
- 3个转轴$b_1, b_2, b_3$
- 原点$C$
- $L$为旋翼到质心的距离
- 这个体系描述了这样一种运动
- 刚体从O点移动到C点,并且进行了旋转变换,此时由于随体系与刚体保持不动,因此随体系坐标不变,而随体系相对于惯性系存在变化,因此旋转矩阵是描述刚体旋转后的惯性系坐标变换
- 旋转矩阵$\mathbf{R}$[同一个点到两个坐标系的运算]
- 欧拉角[刚体的转动可以视为绕不同的轴,独立转动3次]
- 如果不考虑位移[位移可以通过向量加法单独运算],那么刚体仅存在旋转运动
- Z-X-Y顺序旋转[顺序不一定是Z-X-Y,也可能是Z-X-Z或其他,但运算矩阵要一致]
- 旋转矩阵$R$
-
$$ \begin{aligned} R &= R_{Z(\psi)}R_{X(\phi)}R_{Y(\theta)}\\ &=\begin{bmatrix} \cos{(\psi)} & -\sin{(\psi)} & 0\\ \sin{(\psi)} & \cos{(\psi)} & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&\cos{(\phi)} & -\sin{(\phi)}\\ 0&\sin{(\phi)} & \cos{(\phi)}\\ \end{bmatrix} \begin{bmatrix} \cos{(\theta )} & 0 & \sin{(\theta )}\\ 0 & 1 & 0\\ - \sin{(\theta)} & 0 & \cos{(\theta )} \end{bmatrix}\\ &=\begin{bmatrix}- s(\theta ) s(\phi ) s(\psi ) + c(\theta ) c(\psi ) & - s(\psi ) c(\phi ) & s(\theta ) c(\psi ) + s(\phi ) s(\psi ) c(\theta )\\s(\theta ) s(\phi ) c(\psi ) + s(\psi ) c(\theta ) & c(\phi ) c(\psi ) & s(\theta ) s(\psi ) - s(\phi ) c(\theta ) c(\psi )\\- s(\theta ) c(\phi ) & s(\phi ) & c(\theta ) c(\phi )\end{bmatrix}&\text{$s\rightarrow \sin, c \rightarrow \cos$} \end{aligned} $$
- 初始时,假定$\mathbf{p}$为惯性系坐标,此时惯性系和随体系并未发生变换,因此,$\mathbf{p}$也可以表示随体系坐标,当刚体发生旋转后,随体系下坐标并未发生变化,$\mathbf{q}=R\mathbf{p}$描述了随体系坐标到新的惯性系坐标的变换
- 速度
-
$$ \begin{aligned} \dot \mathbf{q}&=\dot R\mathbf{p} + R\mathbf{\dot p}\\ &=\dot R\mathbf{p}&\text{$\mathbf{p}$为常数时,$\dot \mathbf{q}=0$}\\ \end{aligned} $$
- 此时旋转后的点的速度仅取决于$R$对于时间$t$的导数
- $R^T\dot \mathbf{q} = R^T\dot R\mathbf{p}$, 两侧同时乘$R^T$, 即旋转矩阵的逆操作
- $R^T\dot \mathbf{q}$为随体系中的速度
- $R^T\dot R$为随体系的角速度,记为$\hat \omega^b$
- $b$表示body frame
- $\hat \omega$是一种特殊记法,由于角速度中仅有3个独立的量,而$R^T\dot R$表示一个矩阵,为了简便记录,用$\hat \omega$代替
- 若$\omega = [\omega_1, \omega_2, \omega_3]$ $\hat \omega = \begin{bmatrix}0&-\omega_3&\omega_2\\\omega_3&0&-\omega_1\\-\omega_2&\omega_1&0\end{bmatrix}$
- 又有
$\begin{aligned}
\dot \mathbf{q} &= \dot R\mathbf{p}\\
&=\dot RR^T\mathbf{q}&\text{$\mathbf{p}$为$\mathbf{q}$的逆向旋转}
\end{aligned}$
- $\dot \mathbf{q}$为惯性系速度
- $\dot RR^T$为惯性系角速度,记为$\hat \omega^s$
- $s$表示spatial[空间]
-
- 角速度计算
- 以$z$轴为例子
-
$$ \begin{aligned} R_{z(\psi)} &= \begin{bmatrix} \cos{(\psi)} & -\sin{(\psi)} & 0\\ \sin{(\psi)} & \cos{(\psi)} & 0\\ 0 & 0 & 1 \end{bmatrix}\\ \hat \omega^b &=R^T\dot R\\ &= \begin{bmatrix} \cos{(\psi)} & \sin{(\psi)} & 0\\ -\sin{(\psi)} & \cos{(\psi)} & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -\sin{(\psi)} & \cos{(\psi)} & 0\\ \cos{(\psi)} & -\sin{(\psi)} & 0\\ 0 & 0 & 0 \end{bmatrix}\dot \psi\\ &=\begin{bmatrix} 0&-1&0\\ 1&0&0\\ 0&0&0 \end{bmatrix}\dot \psi\\ \hat \omega^s&=\dot RR^T\\ &=\dot \psi\begin{bmatrix} -\sin{(\psi)} & \cos{(\psi)} & 0\\ \cos{(\psi)} & -\sin{(\psi)} & 0\\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \cos{(\psi)} & \sin{(\psi)} & 0\\ -\sin{(\psi)} & \cos{(\psi)} & 0\\ 0 & 0 & 1 \end{bmatrix}\\ &=\dot \psi\begin{bmatrix} 0&-1&0\\ 1&0&0\\ 0&0&0 \end{bmatrix}\\ \end{aligned} $$
- 此时因为旋转轴为$z$, 注意向量上方的$\hat {\omega}$ $\hat \omega^b=\hat \omega^s=\hat{\begin{bmatrix}0\\0\\1\end{bmatrix}}$
-
- 多轴例子[由于转轴非常轴,因此两个参考系内的结果并不一样]
-
$$ \begin{aligned} R&= R_{Z(\psi)}R_{X(\phi)}R_{Y(\theta)}\\ \hat \omega^b&=R^T\dot R\\ &=(R_ZR_XR_Y)^T(\dot R_ZR_XR_Y + R_Z\dot R_X R_Y + R_ZR_X\dot R_Y)\\ &=R_Y^TR_X^TR_Z^T(\dot R_ZR_XR_Y + R_Z\dot R_X R_Y + R_ZR_X\dot R_Y)\\ &=R_Y^TR_X^TR_Z^T\dot R_ZR_XR_Y+R_Y^TR_X^T\dot R_XR_Y + R_Y^T\dot R_Y\\ \hat \omega^s&=\dot RR^T\\ &=(\dot R_ZR_XR_Y + R_Z\dot R_X R_Y + R_ZR_X\dot R_Y)(R_ZR_XR_Y)^T\\ &=(\dot R_ZR_XR_Y + R_Z\dot R_X R_Y + R_ZR_X\dot R_Y)R_Y^TR_X^TR_Z^T\\ &=\dot R_ZR_Z^T + R_Z\dot R_XR_X^TR_Z^T+R_ZR_X\dot R_YR_Y^TR_X^TR_Z^T \end{aligned} $$
-
- 无人机角速度推导
- 参考文章 - zinghd.gitee.io
- 欧拉角速度与角速度的关系推导——欧拉运动方程 (存在公式错误)
- (番外)姿态与旋转矩阵(II) - Tam Alex的文章 - 知乎
- 使用上述文章的推导(与文章推导结果不一致,需要取逆或转置)
-
$$ \begin{aligned} \begin{bmatrix} p\\ q\\ r \end{bmatrix} &= (R_XR_Y)^T \begin{bmatrix} 0\\0\\\dot \psi \end{bmatrix} + R_Y^T \begin{bmatrix} \dot\phi\\0\\0 \end{bmatrix} + \begin{bmatrix} 0\\\dot \theta\\0 \end{bmatrix}\\ &=\begin{bmatrix} c\theta&0&-c\phi s\theta\\ 0&1&s\phi\\ s\theta&0&c\phi c\theta \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi\\ \end{bmatrix} \end{aligned} $$
-
- 直接使用$\hat \omega$公式
-
$$ \begin{aligned} \hat \omega^s&=\dot R_ZR_Z^T + R_Z\dot R_XR_X^TR_Z^T+R_ZR_X\dot R_YR_Y^TR_X^TR_Z^T\\ &=\begin{bmatrix} 0 & - \dot \psi - \dot \theta s{(\phi )} & \dot \phi s{(\psi )} + \dot \theta c{(\phi )} c{(\psi )}\\ \dot \psi + \dot \theta s{(\phi )} & 0 & - \dot \phi c{(\psi )} + \dot \theta s{(\psi )} c{(\phi )}\\- \dot \phi s{(\psi )} - \dot \theta c{(\phi )} c{(\psi )} & \dot \phi c{(\psi )} - \dot \theta s{(\psi )} c{(\phi )} & 0 \end{bmatrix}\\ &=\hat { \begin{bmatrix} \dot \phi c{(\psi )} - \dot \theta s{(\psi )} c{(\phi )}\\ \dot \phi s{(\psi )} + \dot \theta c{(\phi )} c{(\psi )}\\ \dot \psi + \dot \theta s{(\phi )} \end{bmatrix}}&\text{注意符号}\\ &=\hat { \begin{bmatrix} c(\psi)&-s(\psi)c(\phi)&0\\ s(\psi)&c(\phi)s(\phi)&0\\ 0&s(\phi)&1 \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi \end{bmatrix} }\\ \omega^s&=\begin{bmatrix} c(\psi)&-s(\psi)c(\phi)&0\\ s(\psi)&c(\phi)s(\phi)&0\\ 0&s(\phi)&1 \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi \end{bmatrix}\\ \hat \omega^b&=R_Y^TR_X^TR_Z^T\dot R_ZR_XR_Y+R_Y^TR_X^T\dot R_XR_Y + R_Y^T\dot R_Y\\ &=\begin{bmatrix} 0 & - \dot \phi s{(\theta )} - \dot \psi c{(\phi )} c{(\theta )} & \dot \psi s{(\phi )} + \dot \theta\\ \dot \phi s{(\theta )} + \dot \psi c{(\phi )} c{(\theta )} & 0 & - \dot \phi c{(\theta )} + \dot \psi s{(\theta )} c{(\phi )}\\ - \dot \psi s{(\phi )} - \dot \theta & \dot \phi c{(\theta )} - \dot \psi s{(\theta )} c{(\phi )} & 0\end{bmatrix}\\ &=\hat { \begin{bmatrix} \dot \phi c{(\theta )} - \dot \psi s{(\theta )} c{(\phi )}\\ \dot \psi s{(\phi )} + \dot \theta\\ \dot \phi s{(\theta )} + \dot \psi c{(\phi )} c{(\theta )} \end{bmatrix}}&\text{注意符号}\\ &=\hat { \begin{bmatrix} c(\theta)&0&-s(\theta)c(\phi)\\ 0&1&s(\phi)\\ s(\theta)&0&c(\phi)c(\theta) \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi \end{bmatrix} }\\ \omega^b&=\begin{bmatrix} c(\theta)&0&-s(\theta)c(\phi)\\ 0&1&s(\phi)\\ s(\theta)&0&c(\phi)c(\theta) \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi \end{bmatrix} \end{aligned} $$
-
- 使用上述文章的推导(与文章推导结果不一致,需要取逆或转置)
- 以$z$轴为例子
- 牛顿欧拉方程[Newton-Euler’s Equation]
- 牛顿方程
$\mathbf{r}=\begin{bmatrix}
x\\y\\z
\end{bmatrix}$
-
$$ \begin{aligned} m\mathbf{\ddot r} &= R\begin{bmatrix} 0\\0\\F_1+F_2+F_3+F_4 \end{bmatrix}-\begin{bmatrix}0\\0\\mg\end{bmatrix}\\ &= R\begin{bmatrix} 0\\0\\u_1 \end{bmatrix}-\begin{bmatrix}0\\0\\mg\end{bmatrix}\\ \end{aligned} $$
-
- 欧拉方程 $\begin{aligned} I \begin{bmatrix} \dot p\\ \dot q\\ \dot r \end{bmatrix} &=\begin{bmatrix} L(F_2-F_4)\\ L(F_3-F_1)\\ M_1-M_2+M_3-M_4 \end{bmatrix}- \begin{bmatrix} p\\ q\\ r\\ \end{bmatrix} \times I \begin{bmatrix} p\\q\\r \end{bmatrix}\\ &=\begin{bmatrix} 0&L&0&L\\ -L&0&L&0\\ \gamma&-\gamma&\gamma&-\gamma \end{bmatrix} \begin{bmatrix} F_1\\F_2\\F_3\\F_4 \end{bmatrix} - \begin{bmatrix} p\\ q\\ r\\ \end{bmatrix} \times I \begin{bmatrix} p\\q\\r \end{bmatrix}&\text{$\gamma=\frac{k_M}{k_F}$, 无人机的参数,用于计算转动惯量}\\ \mathbf{u_2}&=\begin{bmatrix} 0&L&0&L\\ -L&0&L&0\\ \gamma&-\gamma&\gamma&-\gamma \end{bmatrix} \begin{bmatrix} F_1\\F_2\\F_3\\F_4 \end{bmatrix}\\ I_{xx}\ddot \phi &= L(F_2-F_4)&\text{角加速度} \end{aligned}$
- 牛顿方程
$\mathbf{r}=\begin{bmatrix}
x\\y\\z
\end{bmatrix}$


