准备看点摄像机视觉
Week1
Camera Modeling

- $\frac{1}{f} = \frac{1}{a} + \frac{1}{b}$
- $f$焦距, $a$, 物体到透镜的位置, $b$, 透镜到成像的位置
- $\frac{Y}{a}=\frac{y}{b}$
Single View Geometry
- 平面图到透视图
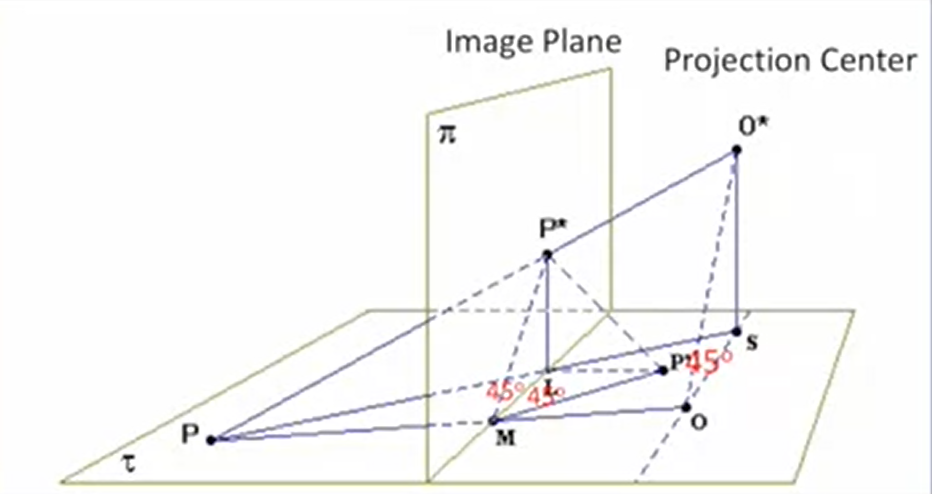
- $o^\star$为眼睛位置
- $S$为垂足
- $OS=O^\star$, 因此$\angle{SOO^\star}=45\degree$
- $P$为平面图上一点
- 连接$P-O$交图像平面$M$
- 连接$P-O^\star$交图像平面$P^\star$
- $\triangle MLP^\star\sim\triangle OSO^\star$
- $\angle LMP’$为$45\degree$
- $\triangle MLP^\star=\triangle MLP’$, 即,将成像面的点$P^\star$映射到平面$P’$变为透视图
- 因此,$P’$是$P$关于$ML$对称的透视图
- 多透视点画法Kim Jung Gi
- 投影面[Projective Plane]
- 投影面上的点$(x,y)$可以视为,视点向外发出的射线$(s_x, s_y, s)$
- homogeneous coordinates[齐次坐标]
- 引入新的维度,表示无限远处的坐标
- $(x,y)\rightarrow(x,y,1)$, $1$表示投影面距离
- $(x,y,0)$表示无限远处的点
- $(0,0,1)$表示无限远处的线
- 投影面上的直线
- $ax+by+c=0$
- vector notation
$0=\begin{bmatrix}
a&b&c
\end{bmatrix}\begin{bmatrix}
x\\y\\1
\end{bmatrix}$
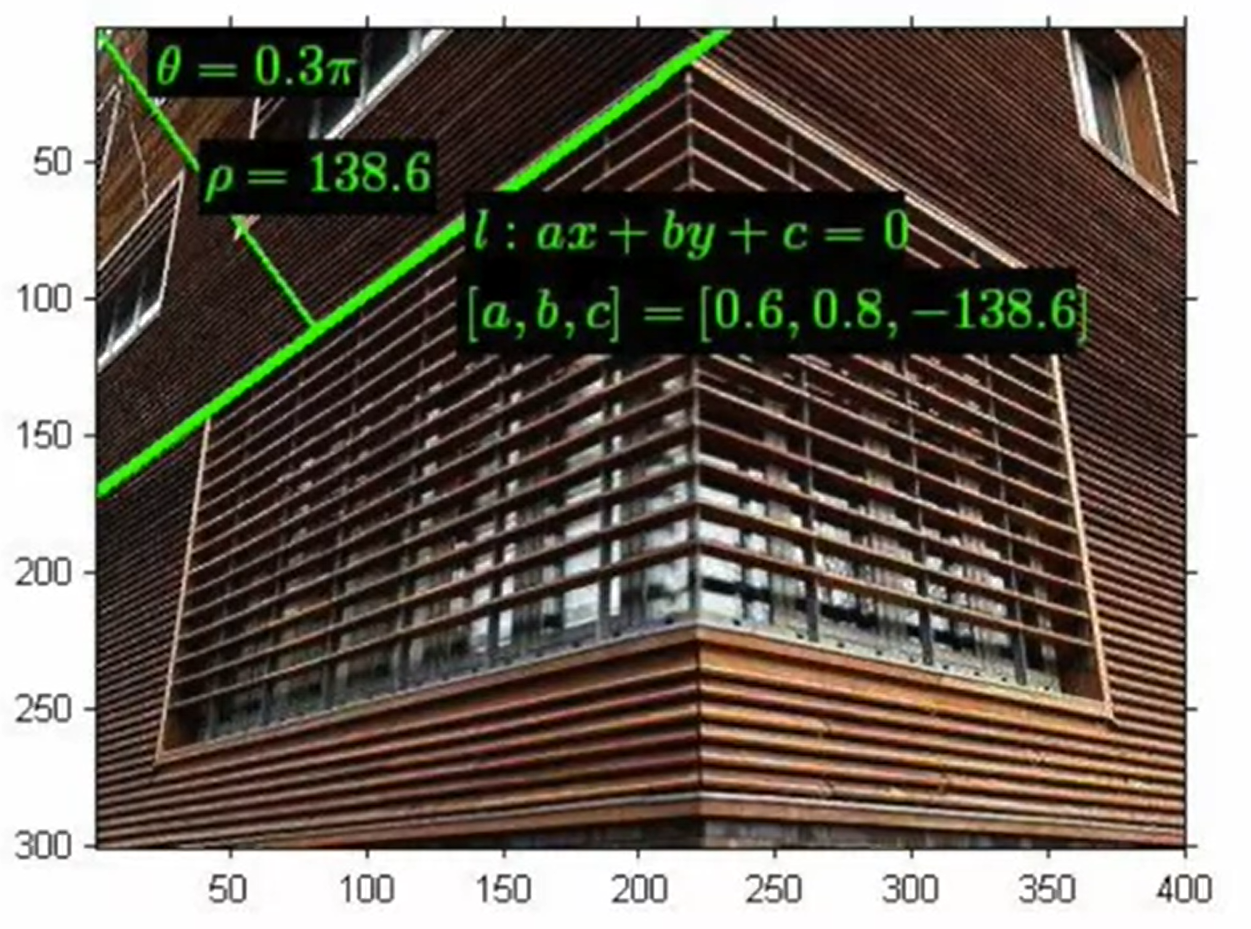
- 极坐标$\rho = x\cos\theta + y\sin\theta$
- $\rho$原点到直线的距离
- $\theta$线与x夹角
- $\cos\theta = \frac{a}{\sqrt{a^2+b^2}}$
- $\sin\theta = \frac{b}{\sqrt{a^2+b^2}}$
- $\rho = -\frac{c}{\sqrt{a^2+b^2}}$
- 叉乘法
- 点$A=(x_1, y_1, 1)$, 点$B=(x_2, y_2, 1)$
- 想象AB分别为视点发出的两个射线与投影面相交,则$A\times B$为一平面的法向量,法向量与投影面相交即为投影面直线
- 标准化$I=\frac{A\times B}{|A\times B|}$
- 其次化$I=\frac{A\times B}{[A\times B]_{[3]}}$
- 旋转和平移
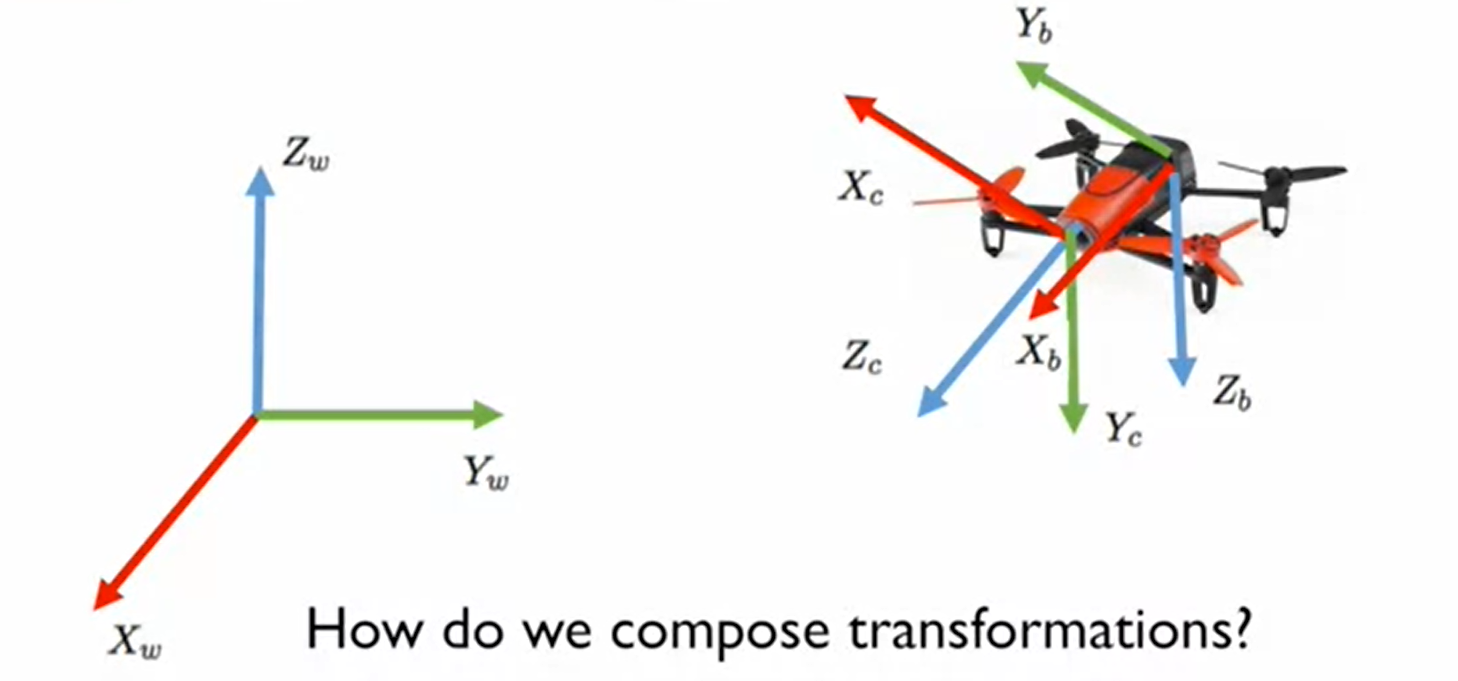
- $[X_w, Y_w, Z_w]$ 世界坐标系 world coordinate
- $[X_c, Y_c, Z_c]$ 相机坐标系 camera coordinate
- $[X_b, Y_b, Z_b]$ 机体坐标系 body coordinate
- $^cP$ 相机坐标,$^wP$世界坐标
- ${}^cP={}^cP_w{}^wP+{}^cT_w$
- Pinhole Camera Model[小孔成像模型]
- Dolly room
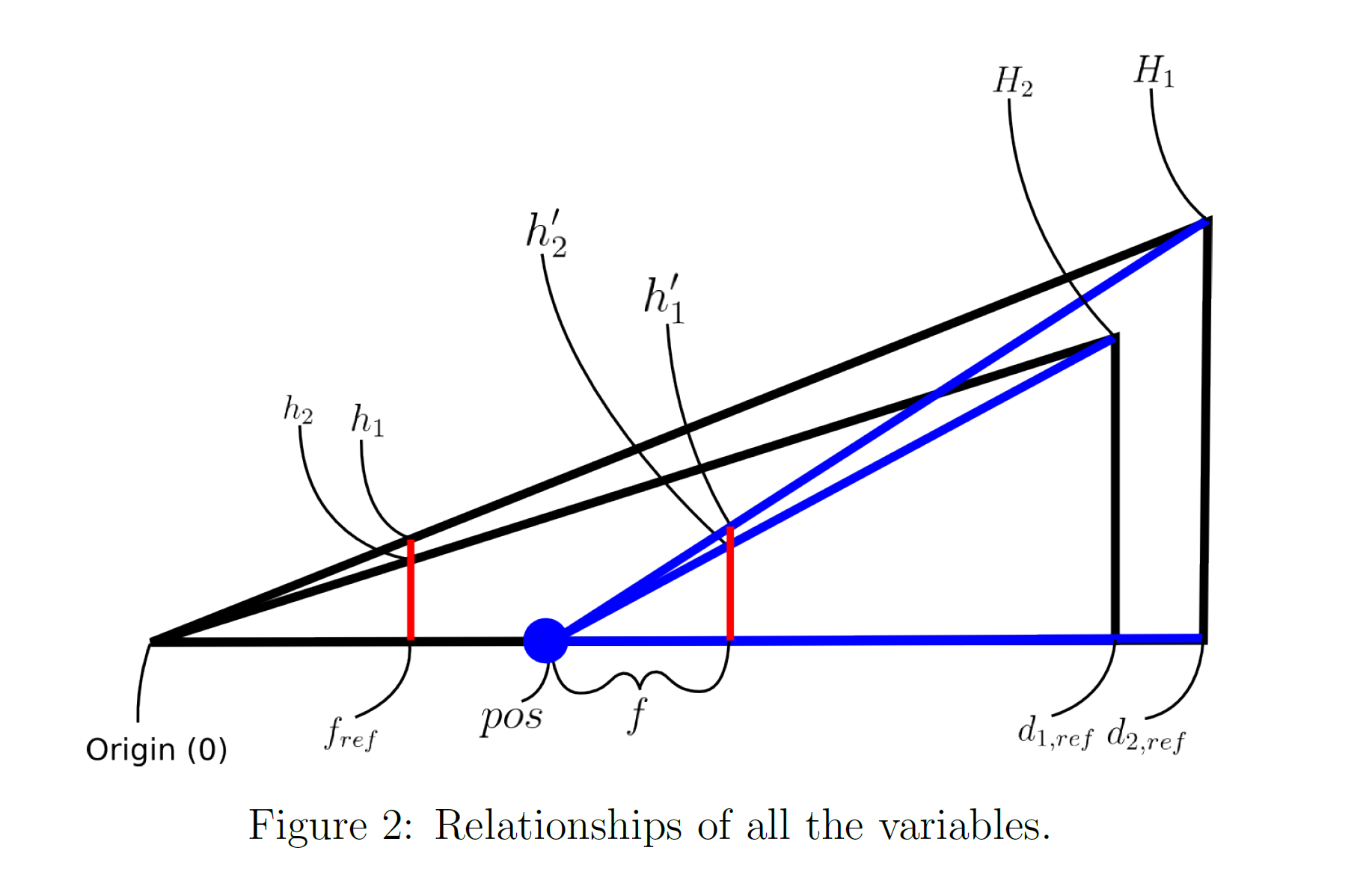
- 相机从$O$点向右移动$pos$, 成像面,$h_1=h_1’$
- $ref$表示移动前的数据
- 物体高度$H_1,H_2$
- 若已知$H_1, pos, d_{1,ref}$ 求 $f$
-
$$
\begin{aligned}
\frac{h_1}{f_{ref}} = \frac{H_1}{d_{1,ref}}&, \frac{h_1'}{f} = \frac{H_1}{d_{1,ref}-pos}\\
\frac{f_{ref}}{d_{1,ref}}&=\frac{f}{d_{1,ref}-pos}\\
f &= (d_{1,ref}-pos)\frac{f_{ref}}{d_{1,ref}}
\end{aligned}
$$
- 若已知$H_1, H_2, d_{1,ref}, d_{2,ref}, r=\frac{h_1’}{h_2’}, f_{ref}$,求$f, pos$, 利用一个像的大小不变,移动相机, 根据另外一个像的比例,计算焦距和移动距离
-
$$
\begin{aligned}
&\begin{cases}
\frac{H_1}{d_{1,ref}}&=\frac{h_1}{f_{ref}}&(1)\\
\frac{H_2}{d_{2,ref}}&=\frac{h_2}{f_{ref}}&(2)\\
\frac{H_1}{d_{1,ref}-pos}&=\frac{h_1'}{f}&(3)\\
\frac{H_2}{d_{2,ref}-pos}&=\frac{h_2'}{f}&(4)\\
\end{cases}\\
\frac{h_1}{f}&=\frac{H_1}{d_{1,ref}-pos}=r\frac{H_2}{d_{2,ref}-pos}&(3)(4)联立\\
pos&=\frac{rH_2d_{1,ref} - H_1d_{2,ref}}{rH_2-H_1}\\
h_1&=f_{ref}\frac{H_1}{d_{1,ref}}=rf\frac{H_2}{d_{2,ref} - pos}&(1)(3)联立\\
f &= (d_{1,ref}-pos)\frac{f_{ref}}{d_{1,ref}}
\end{aligned}
$$
- Compute intrinsics from vanishing point
- image center
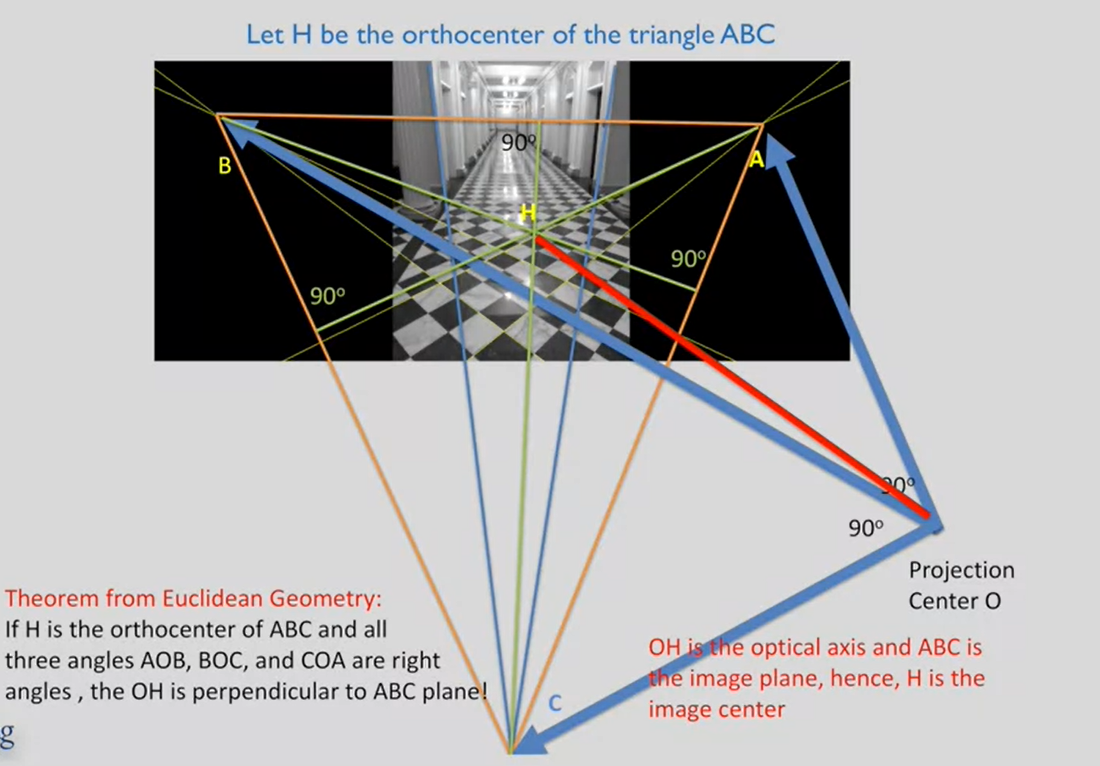
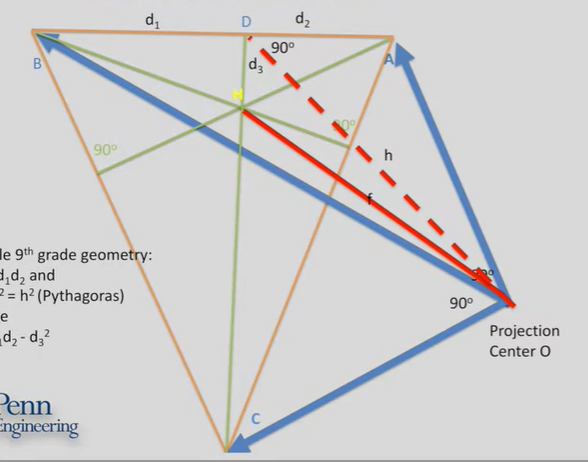
- $A,B,C$, 灭点
- $AB$, 地平线
- $C$, 垂线灭点
- $O$, 相机投影中心
- $\angle BOC=\angle AOC=\angle AOB=90\degree$
- $H$为$\triangle ABC$垂心
- $OH\perp \triangle ABC$
- $H$为image center
- force length