Robotics-Perception-Week3

Visual Features[视觉特征提取]

SIFT [Scale-invariant feature transform] 尺度不变特征转换

• 大致思想
• 我们需要同一个相机按不同视角拍摄的同一处的画面
• 类似于全景图
• 在拼接全景图时，我们需要找到对应的特征点，才能方便图片对接
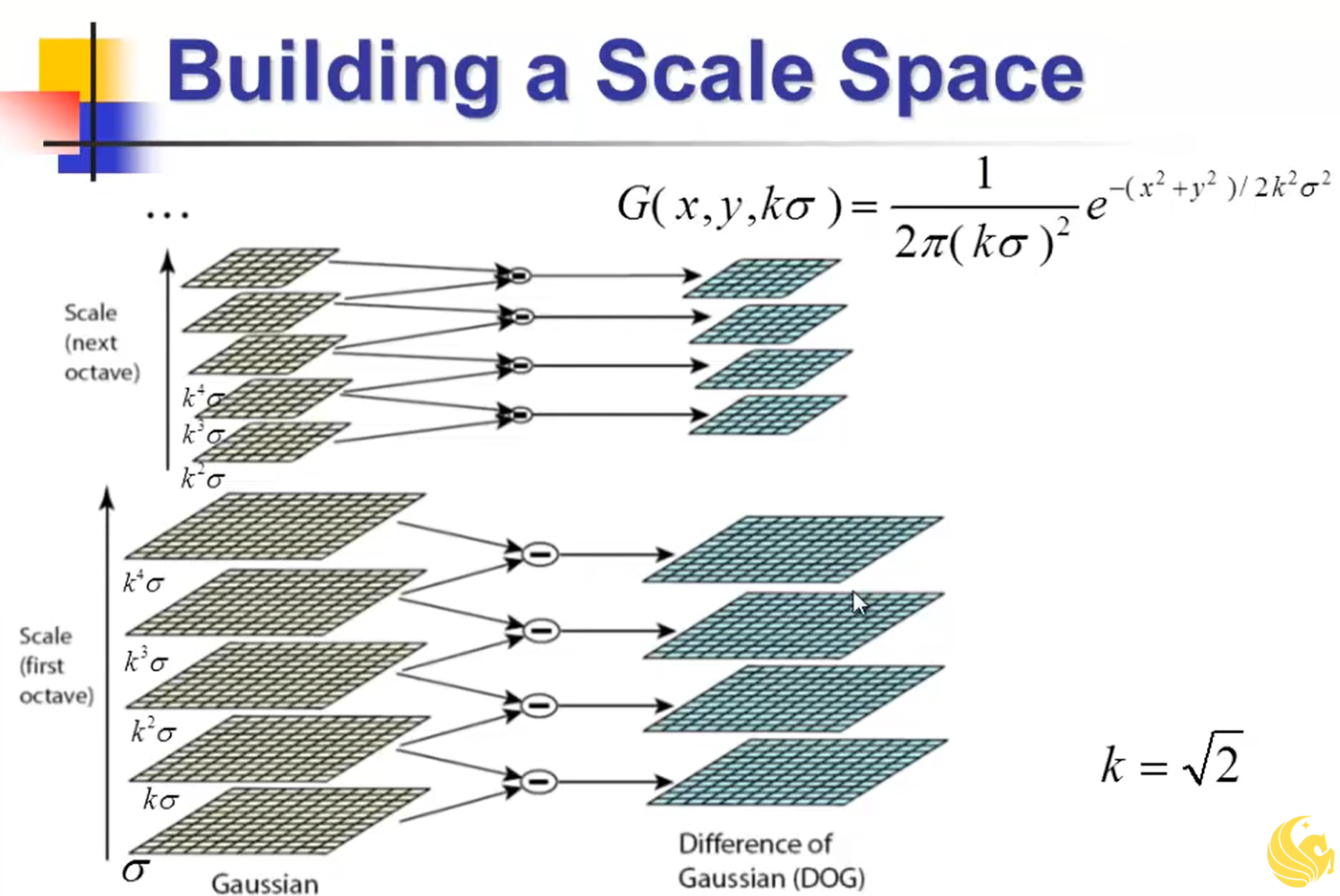
• SIFT即为一种寻找特征点的算法
• 对于一张图片进行不同$\sigma=1, \sqrt{2}, 2, \dotsc$的二维高斯卷积得到一组(octive)
• 再将这张图片进行降采样(隔点采样)，拿到缩水的图片
• 对于缩水的图片再次进行卷积，使用的$2\sigma=2, 2\sqrt{2}, 4 \dotsc$
• 对于同一组(octive)的图片，相邻两张做差，得到DoG Difference of Gaussian, 其实是一种LoG laplacian of gaussian的近似

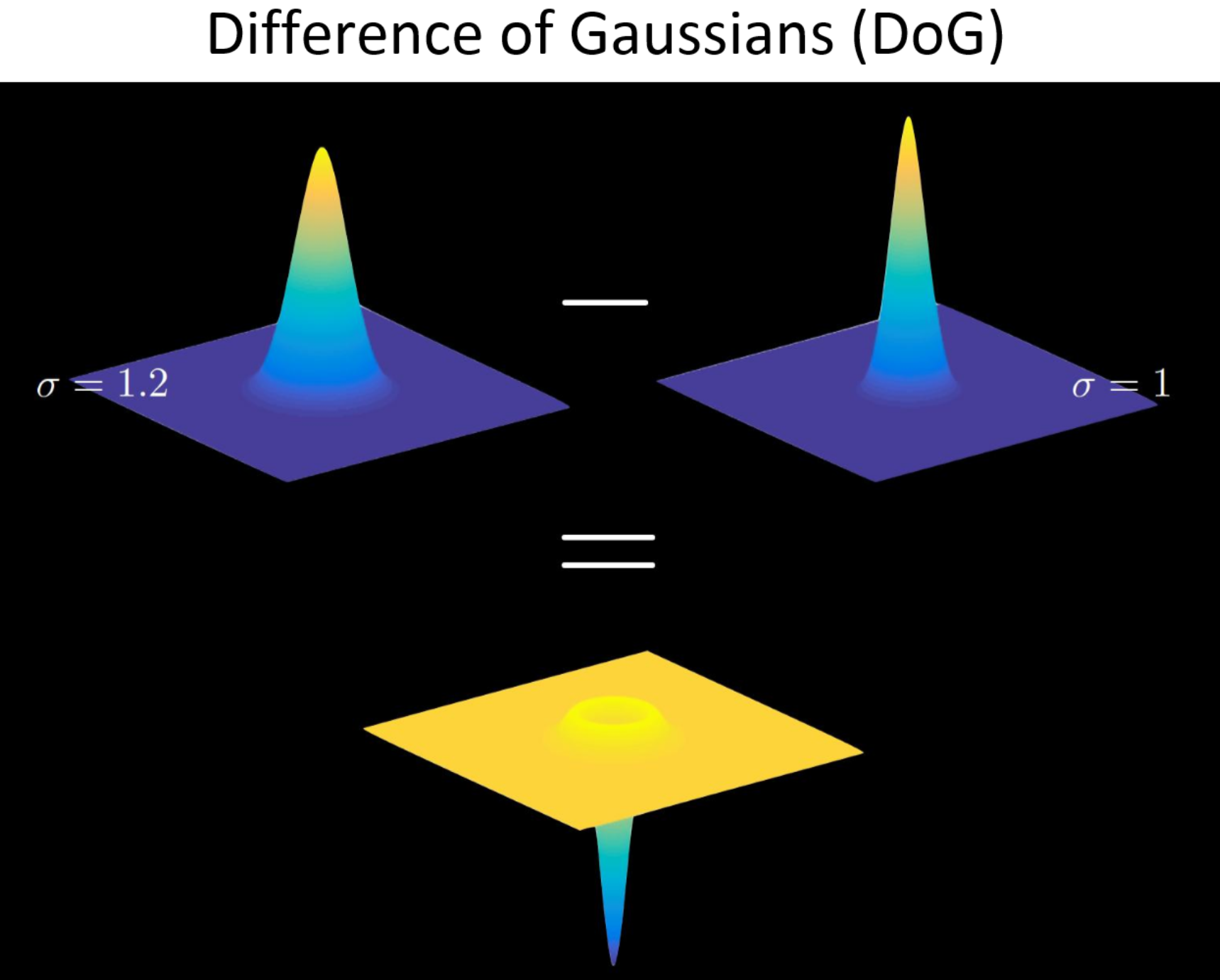
Gaussian pyramid[高斯金字塔]

• 迭代(高斯卷积->降采样->得到一个长宽只有$\frac{1}{2}$的图)

拉普拉斯金字塔

Sift算法中的多尺度金字塔

差分金字塔与Difference of Gaussian(DOG)高斯函数的差分

同时，需要归一化，以避免信号流式

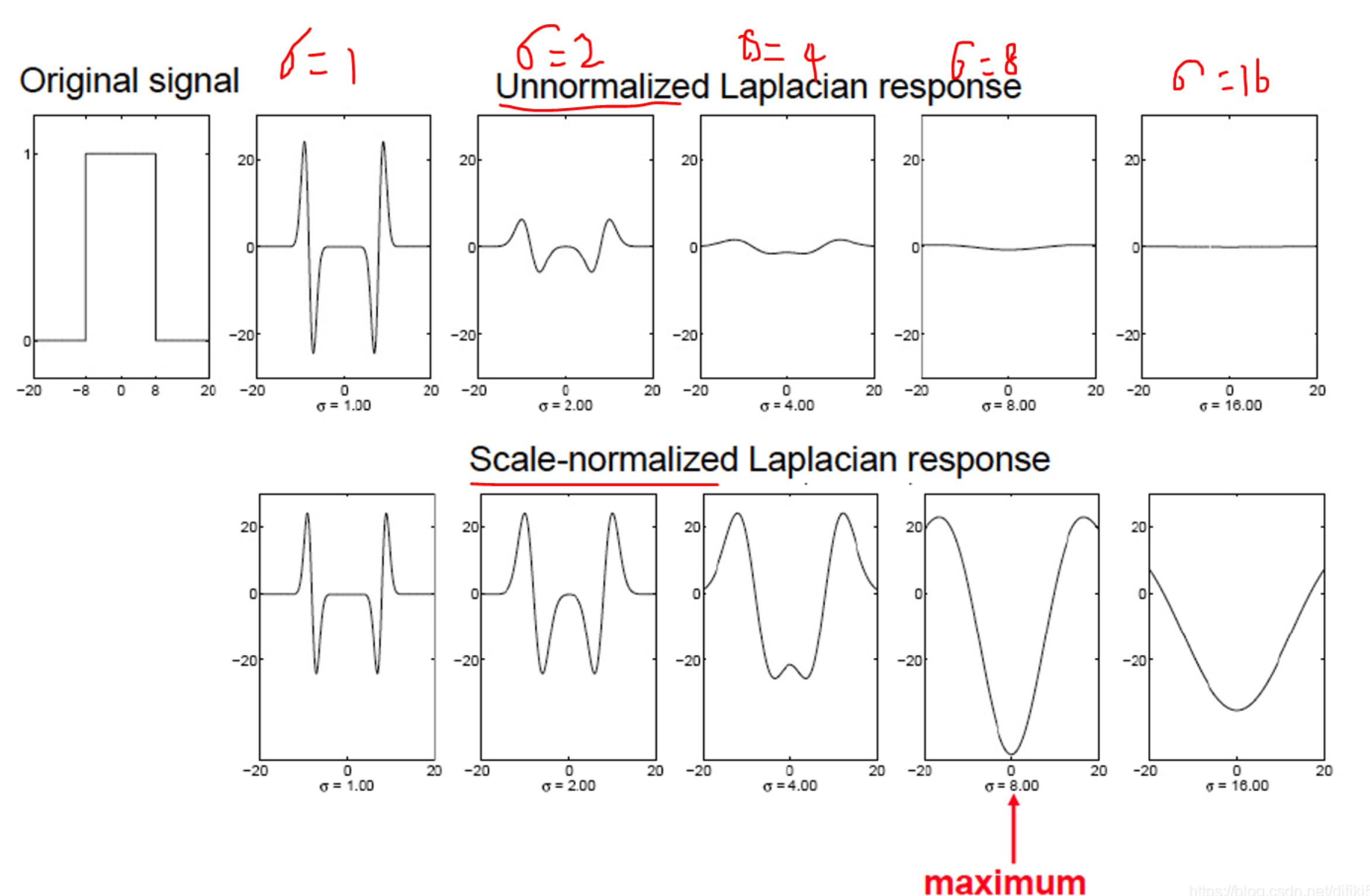
拿到的最大响应点即我们需要的特征点

Reference

• zhaoxuhui.top
• 图像特征尺度不变性-拉普拉斯-高斯差DOG-SIFT特征提取-旋转不变性-SVD分析-齐次坐标的理解-线性的理解-齐次方程的理解 CSDN
• 🤙SIFT算法详解 - zddblog[CSDN]
• 🤙SIFT算法原理详解 - Alliswell-WP[cnblogs]
• 🤙UCF Computer Vision Video Lectures 2012[5] - Dr. Mubarak Shah[Youtube]

SVD

• $A_{m\times n}=U_{m\times m}D_{m\times n}V_{n\times n}^T$
• $U$, 每列正交
• $V$, 正交

平均脸

• 把每张图片按$1\times n$重新排列
• 组成一个$n\times N$的矩阵
• 通过SVD分解，拿到前几个特征，进行重构后即可

• 改变$D$的元素个数，可以更改$A$的秩
• 使$D$取倒数，则可计算$A^{-1}=VD^{-1}U^T$
• $D$非负