Review of Robotics Perception week1
Review of week 1
First Person Camera World
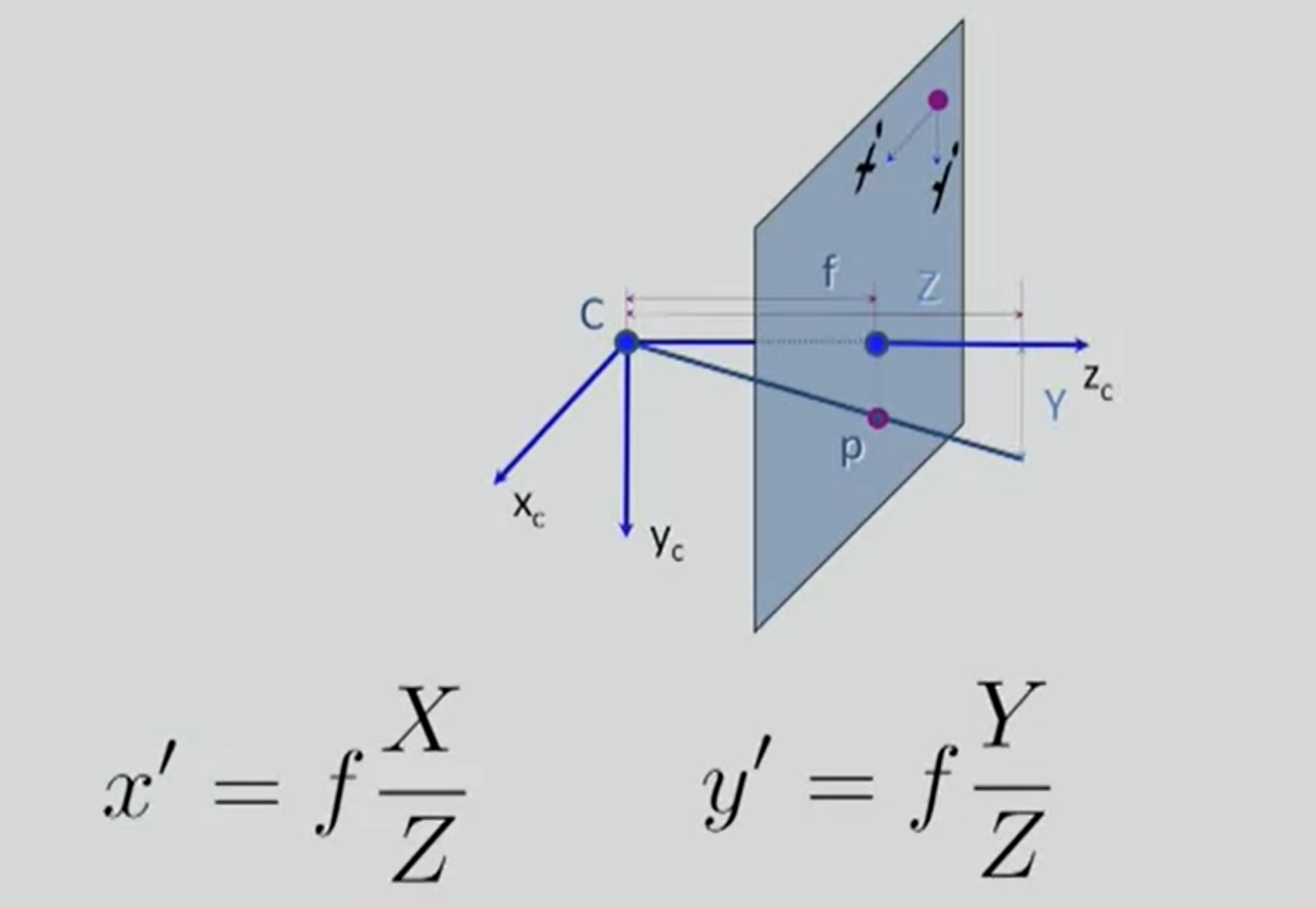
- $x’, y’$ 为投影面坐标
- $X,Y$ 为物体实际坐标
- $Z$为物体距离原点距离
- $C$为第一视角原点
- $f$为焦距
- 投影面为一个虚像，真实成像是个倒像，但大小一致
- $x’=f\frac{X}{Z}, y’=f\frac{Y}{Z}$
- 矩阵形式
$$
Z_c
\begin{bmatrix}
x'\\y'\\1
\end{bmatrix}
=
\begin{bmatrix}
f&0&0&0\\
0&f&0&0\\
0&0&1&0\\
\end{bmatrix}
\begin{bmatrix}
X_c\\Y_c\\Z_c\\1
\end{bmatrix}
$$
- 这里的1作为3位空间的齐次项
Conversion form mm to pixels
- 光学中心$O_C,O_r$
- $x’,y’$投影面坐标(像素)
- $c,r$为实际距离
- 缩放加平移之后
- $s_x, s_y$为像素宽
- $c-O_c=\frac{x’}{s_x}, r-O_r=\frac{y’}{s_y}$
- 矩阵形式
$$
\begin{bmatrix}
x\\y\\z
\end{bmatrix}
=\begin{bmatrix}
a_x&s&P_x\\
0&a_y&P_y\\
0&0&1\\
\end{bmatrix}
\begin{bmatrix}
x'\\y'\\z'
\end{bmatrix}
$$
- Here $a_x, a_y$ is two scala factor, 用于表示像素和米的倍数关系
- $P_x, p_y$ is the principle point(where optical axis hits image plane)
- $s$ is the slant factor, when the image plane is not normal to the optical axis
- 就是说，相机的成像面可能和透镜面不平行导致的位差，需要一个参数来纠正
Comine the intrinsic camera parameters
$$
\begin{aligned}
\begin{bmatrix}
x\\y\\z
\end{bmatrix}
&=
\begin{bmatrix}
a_x&s&P_x\\
0&a_y&P_y\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
f&0&0&0\\
0&f&0&0\\
0&0&1&0\\
0&0&0&0\\
\end{bmatrix}
\begin{bmatrix}
x'\\y'\\z'
\end{bmatrix}\\
&=
\begin{bmatrix}
a_xf&sf&P_x\\
0&a_yf&P_y\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x'\\y'\\z'
\end{bmatrix}\\
\end{aligned}
$$
- Mark $K$ as Calibration matrix
$$
K=\begin{bmatrix}
a_xf&sf&P_x\\
0&a_yf&P_y\\
0&0&1
\end{bmatrix}
$$
- From 3D World in first person view to 2D pixel in first persion view
$$
Z\begin{bmatrix}
u_{img}\\v_{img}\\1
\end{bmatrix}
=
\begin{bmatrix}
f_x&s&p_x\\
&f_y&p_y\\
&&1
\end{bmatrix}
\begin{bmatrix}
\mathbf{I_{3*3}}&\mathbf{0}
\end{bmatrix}
\begin{bmatrix}
X_{cam}\\Y_{cam}\\Z_{cam}\\1
\end{bmatrix}
$$
Third Person to First person 3d mappgin
- 旋转加平移 $\mathbf{X_c} = \begin{bmatrix} \mathbf{R_{3*3}}&t_{3*1}\\ \mathbf{0}&1 \end{bmatrix} \mathbf{X}$
Combining Internal and External parameters
$$
\begin{aligned}
\mathbf{x} &= \mathbf{K_{3*3}}[\mathbf{I};0]_{3*4}\mathbf{X_c}\\
&=\mathbf{K}
\begin{bmatrix}
\mathbf{R}&t
\end{bmatrix}\mathbf{X}
\end{aligned}
$$
非线性失真
- 用于处理球面映射出现的偏差 $\begin{bmatrix} \mathbf{x}\\1 \end{bmatrix} = L\big (\mathbf{K}\begin{bmatrix} \mathbf{R}&t \end{bmatrix} \begin{bmatrix} \mathbf{X}\\1 \end{bmatrix}\big)$
