Newton Euler Equation
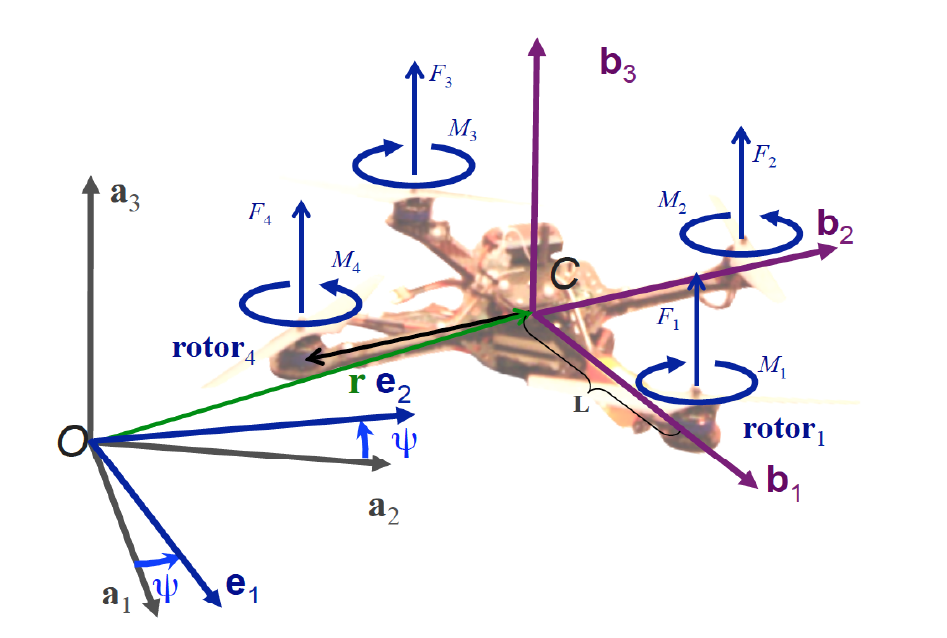
牛顿欧拉方程
Newton Equation
- 计算出4旋翼的作用力在惯性系下的分量
- 无人机在水平状态下,受到向上的推力$F=f_1+f_2+f_3+f_4$和重力$mg$
- 无人机在旋转状态下通过旋转矩阵$R$可以计算出惯性系下3个方向的作用力分量
- 同时由于重力方向不变,可以之间减去,得到
- 其中$R_{ZXY}$为按照$ZXY$3个轴依次旋转得到的矩阵,如果转轴不同,则可能得到不同的表示
- 对应的3个分量为
Euler Equation
- 旋转过程
-
上面的方程分别对$\phi \theta \psi$求导,即可得到体坐标系下的角速度方程 $\begin{bmatrix} p\\q\\r \end{bmatrix} = \begin{bmatrix} c(\theta)&0&-c(\phi)s(\theta)\\ 0&1&s(\phi)\\ s(\theta)&0&c(\phi)c(\theta) \end{bmatrix} \begin{bmatrix} \dot \phi\\ \dot \theta\\ \dot \psi \end{bmatrix}$
- 根据欧拉方程
后面有推导过程,暂时先直接用 $M=\begin{bmatrix} L(F_2-F_4)\\ L(F_3-F_1)\\ M_1-M_2+M_3-M_4 \end{bmatrix} -\begin{bmatrix} p\\q\\r \end{bmatrix} \times I \begin{bmatrix} p\\q\\r \end{bmatrix}$
- 其中
- $M$为力矩
- $L$为马达到质点的距离
- 由于rotor1,3转向相同,和rotor2,4转向相反,根据右手定则,1,3顺时针,力矩向上,2,4逆时针,力矩向下
- 以$b_1$为前进方向,则$F_2,F_4$的大小差决定了无人机的翻转角,$F_1,F_3$同理
- $I$为转动惯量
- 一般情况下,转动惯量为质量与质点的长度积分得到,因此可以认为转动惯量通常只跟形状和质量有关,可以按常量计算,对于使用电池作为动力源的无人机来说比较使用,如果存在油耗或其他质量损失的情况则需要进一步分析
- 将等号右边梳理成矩阵形式,可以写成 $M=I\begin{bmatrix} \dot p\\\dot q\\\dot r\\ \end{bmatrix} = \begin{bmatrix} 0&L&0&-L\\ -L&0&L&0\\ \gamma&-\gamma&\gamma&-\gamma \end{bmatrix} \begin{bmatrix} F_1\\F_2\\F_3\\F_4 \end{bmatrix} - \begin{bmatrix} p\\q\\r \end{bmatrix} \times I \begin{bmatrix} p\\q\\r \end{bmatrix}$
- 其中
- $\times$为叉乘符号
- $\gamma$为力与力矩的比例关系(这里依然用到了惯量不变假设)
- 这里的$p,q,r$依然是以无人机为参考系的角速度
- $I$为转动惯量矩阵 $\begin{bmatrix} I_{xx}&0&0\\ 0&I_{yy}&0\\ 0&0&I_{zz}\\ \end{bmatrix}$
- 拆成分量形式,可以得到 $\begin{aligned} M_x&=I_{xx}\dot p&=&qr(J_{yy}-J_{zz})+L(F_2-F_4)\\ M_y&=I_{yy}\dot q&=&pr(J_{zz}-J_{xx})+L(F_1-F_3)\\ M_z&=I_{zz}\dot r&=&pq(J_{xx}-J_{yy})+L(F_1-F_2+F_3-F_4)\\ \end{aligned}$
牛顿欧拉方程即为
- 其中对于$p,q,r$的计算,若认为无人机角度变化微小,则可以利用$\sin(\theta)\sim\theta, \cos(\theta)\sim1$进行代换
欧拉方程的推导
- 为了便于类比,放一个质点平动和刚体转动的公式对比
- $\dot{}$ 都表示对时间的导数
| 质点 | 刚体 |
|---|---|
| 速度$v=\dot x$ | $\omega=\dot \theta$ |
| 加速度$a=\ddot x$ | $\alpha=\ddot \theta$ |
| 力$F$ | 力矩$M$ |
| 质量$m$ | 转动惯量$I=\int r^2dm$ |
| 动量$p=mv$ | 角动量$L=I\omega$ |
| 牛顿定律$F=\dot p$ | $M=\dot L$ |
-
推导 $\begin{aligned} M&=\dot L\\ &=\dot I\omega + I\dot \omega\\ &=(\dot{\sum_i\sum_jI_{ij}\mathbf{e_i}\mathbf{e_j}})\omega + I\dot \omega\\ &=(\sum_i\sum_j(\dot I_{ij}\mathbf{e_i}\mathbf{e_j}+I_{ij}\mathbf{\dot e_i}\mathbf{e_j}+I_{ij}\mathbf{e_i}\mathbf{\dot e_j}))\omega+I\dot \omega\\ &=(\sum_i\sum_j(I_{ij}\mathbf{\dot e_i}\mathbf{e_j}+I_{ij}\mathbf{e_i}\mathbf{\dot e_j}))\omega+I\dot \omega&\text{认为$\dot I_{ij}=0$}\\ &=\sum_i\sum_j(I_{ij}(\omega\times \mathbf{e_i})\mathbf{e_j}-I_{ij}\mathbf{e_i}(\mathbf{e_j}\times\omega))\omega+I\dot \omega\\ &=(\omega\times I - I\times \omega)\omega+I\dot\omega\\ &=(\omega\times I)\omega - (I\times \omega)\omega+I\dot\omega\\ &=(\omega\times I)\omega+I\dot\omega&\text{$(I\times \omega)\omega=0$}\\ \end{aligned}$
- 当$I_{i\neq j}=0$时,即非对角元素为0
- 有

