Install Remote Browser[remoteview], And Coursera Robotics-Flight week 2

remote chrome debuging

• need ws resever proxy to ws
• trying to use ipv6 access browser directly
• trying to ssh tunnel mapping 9222 to 9223
• still can not fix ws problem

Try to use remoteview[base on npm]

• here is the tutorial
• trying to install remoteview by npm
  • npm i remoteview
    • but can not access the npm offical website
  • trying to npm pack and npm install, still need web access permission.
  • trying download all remoteview package [too complex, I give it up]

准备看点Coursera

• week 2
  • Coursera: robotics-flight
  • Euler angle
    • 对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现
    • 
    • 
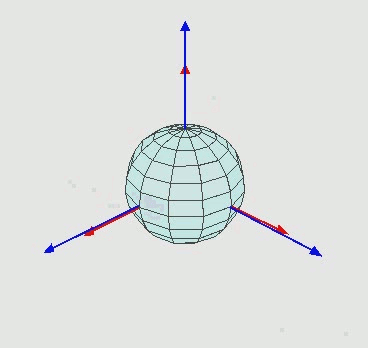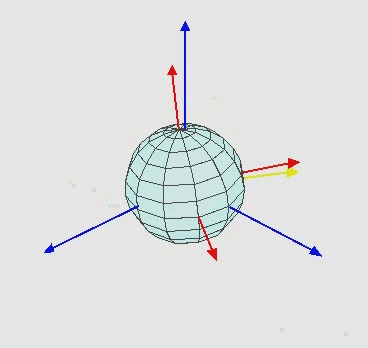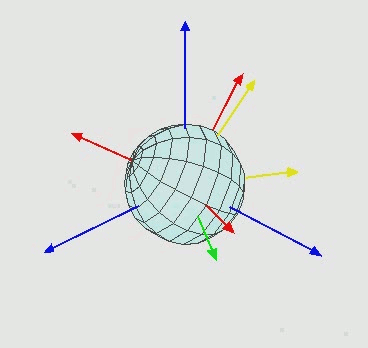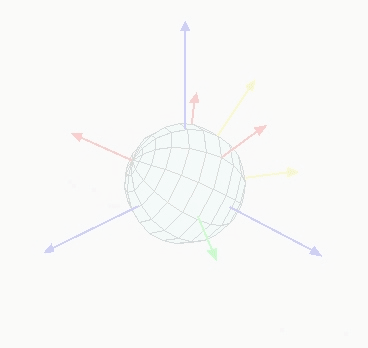
    • 从左到右依次代表绕着z轴的旋转、绕着交点线的旋转、绕着Z轴的旋转。
    • 
  • Rodrigues’ formula [罗德里格旋转公式 at 1840]
    • 是在给定转轴和旋转角度后，旋转一个向量的有效算法
    • here’s $\mathbf{k}$ is unit vector
    • $\mathbf{v_{rot}} = \mathbf{v}\cos\theta + (\mathbf{k}\times\mathbf{v})\sin\theta + \mathbf{k}(\mathbf{k}\cdotp\mathbf{v}(1-\cos\theta))$
      • proof
      • $\begin{aligned} \mathbf{v_{rot}} &= \mathbf{v_{\parallel rot}} + \mathbf{v_{\perp rot}}\\ &= \mathbf{v_{\parallel}} + \cos(\theta)\mathbf{v_{\perp}} + \sin(\theta)\mathbf{k}\times\mathbf{v} \\ &= \mathbf{v_{\parallel}} + \cos(\theta)(\mathbf{v} - \mathbf{v_{\parallel}}) + \sin(\theta)\mathbf{k}\times\mathbf{v} \\ &= \cos(\theta)\mathbf{v} + (1-\cos(\theta))\mathbf{v_{\parallel}} + \sin(\theta)\mathbf{k}\times\mathbf{v} \\ &= \cos(\theta)\mathbf{v} + (1-\cos(\theta))(\mathbf{k}\cdotp\mathbf{v})\mathbf{k} + \sin(\theta)\mathbf{k}\times\mathbf{v} \\ \end{aligned}$
      • calculator the rotation matirx given by $\mathbf{k}$ and $\theta$
      • 
      • 
      • 
      • in term of the matrix exponential
        • 
      • python code

      def make_rotation_matrix(k, theta):
        x, y, z = k
        I = np.eye(3)
        K = np.matrix([
            [0, -z, y],
            [z, 0, -x],
            [-y, x, 0]
        ])
        R = I + np.sin(theta) * K + (1 - np.cos(theta)) * K * K
        return R
      

  • Matrix exponential[矩阵指数]
    • wiki
    • 矩阵的指数函数到底说的是个啥？ - TravorLZH的回答 - 知乎
    • more about pdf
  • Derivative of the rotation matrix
    • $$ \begin{aligned} \frac{d}{dt}(A\pm B) &= \dot A \pm \dot B\\ \frac{d}{dt}(AB) &= \dot A B + A \dot B\\ \frac{d}{dt}(A(\theta(t))) &= \frac{dA}{d\theta}\dot \theta \end{aligned} $$
    • Angular velocity
      • $R^T\dot R = \dot R R^T$
    • Skew - Symmetric Matrices and the Hat Operator
      • symmetric matrix: $A^T = A$
      • skey-symmetric matrix: $A^T = -A$
      • $$ \hat a = \hat{\begin{bmatrix}a_1\\a_2\\a_3\end{bmatrix}} = \begin{bmatrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{bmatrix} $$
      • $\mathbf{u}\times\mathbf{v} = \hat{\mathbf{u}}\mathbf{v}$
      • $\hat\omega^b = R^T\dot R$
      • $\hat\omega^s = \dot RR^T$
  • Newton-Euler Equations
    • [飞控]从零开始建模(一)-牛顿欧拉方程 - zinghd的文章 - 知乎
  • Finish week home work