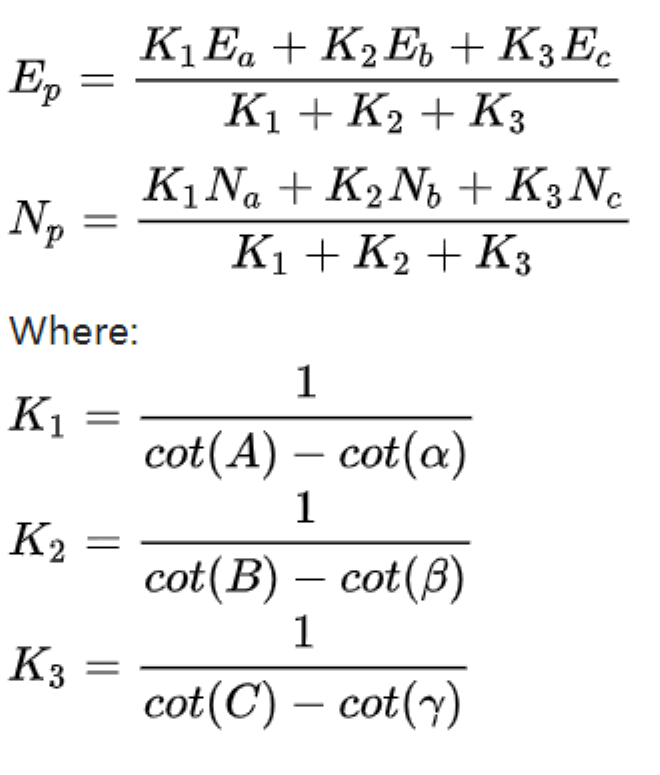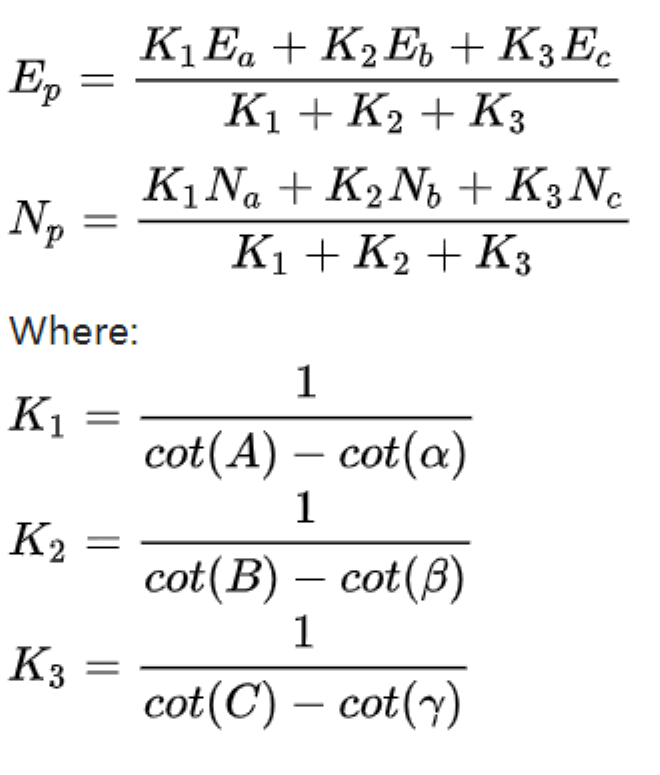RANSAC[Random Sample Consenus]
- 该算法其实是一种迭代选过滤
outliers的思想,并不局限于对点进行拟合
- 通常与
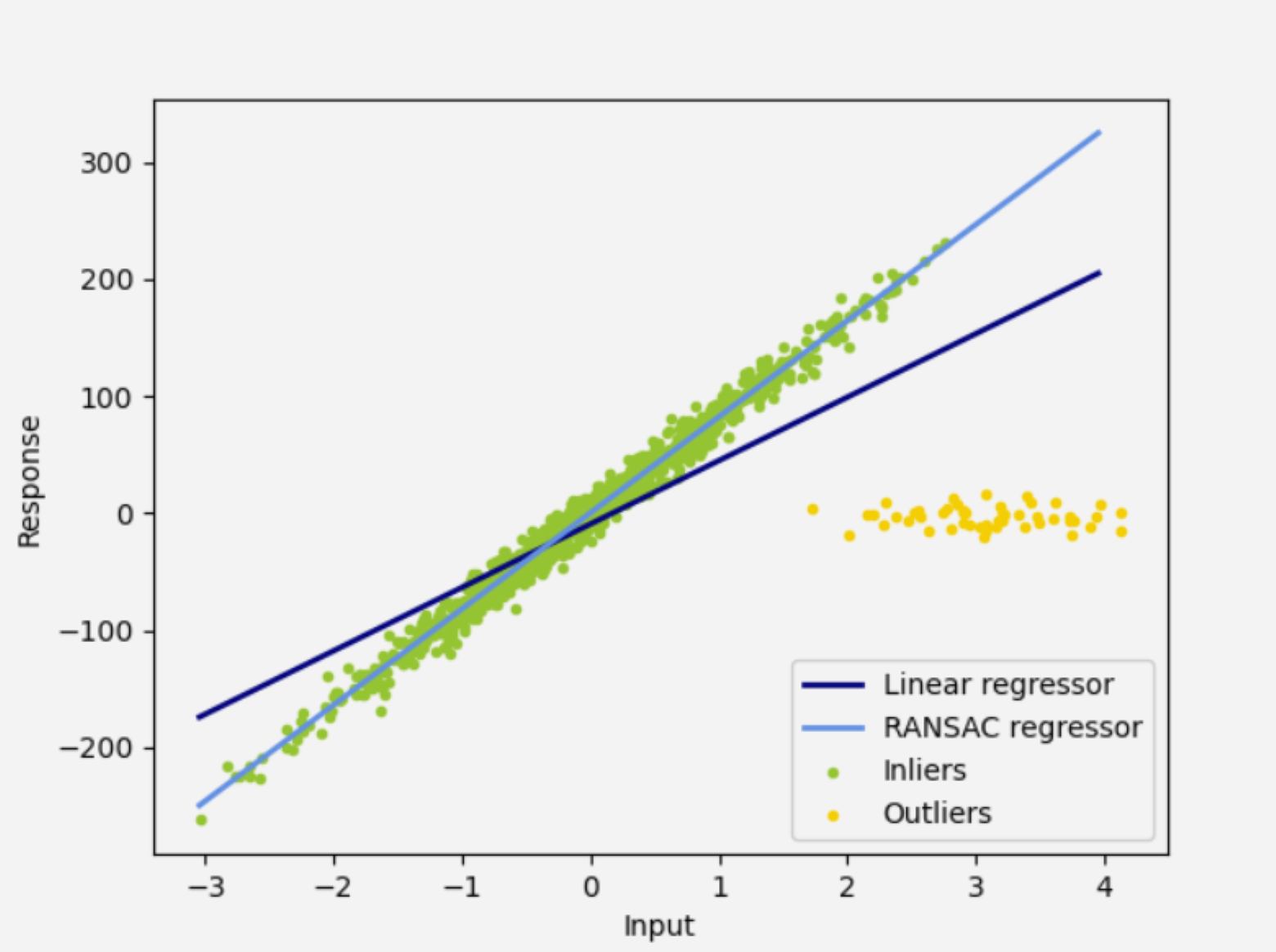
Linear regressor进行对比用于体现Linear regressor的不足之处
- 从信息提供的角度来说
Linear regressor认为每个点所在的位置都是有意义的,即便存在outlier,也不应当将其剔除,因此该算法在遇到outlier距离其他数据很远时,则会显现出倾向于outlier结果- 而
RANSAC则倾向于,多数点同意则完全收敛到点数最多的模型那里,但显然RANSAC在面对两组数据量差不多的模型时,无法单独做出决策,即,在两个模型中反复横跳
- Code at ucas
Orthogonal Procrustes Problem[正交普鲁克问题, 3D-3D pose]
- 一个为了让客人和自己的床一样大小而砍断客人双脚或拉长客人的古希腊故事[普罗克汝斯特斯之床]
- 给定两个矩阵$A$和$B$并要求找到一个正交矩阵$\Omega$最接近映射$A$到$B$
- $R=\underset{\Omega}{\argmin}{\Vert\Omega A-B\Vert}_F\ \ \ \text{subject to}\ \ \ \Omega^T\Omega=I$
- 其中$\Vert X\Vert_F$为Frobenius 范数
- $\Vert X\Vert_F=\sqrt{trace(X^TX)}=\sqrt{\sum_{i,j}x_{ij}^2}$

- 当$S$为单位阵时,表达式可以最大化
- 通常用来解决点云旋转的匹配最优解,(因为旋转变换都是正交阵)
Pose from Point Correspondences P3P
- 当船看到两个灯塔并测得方位角时,可以知道,船在这个圆上
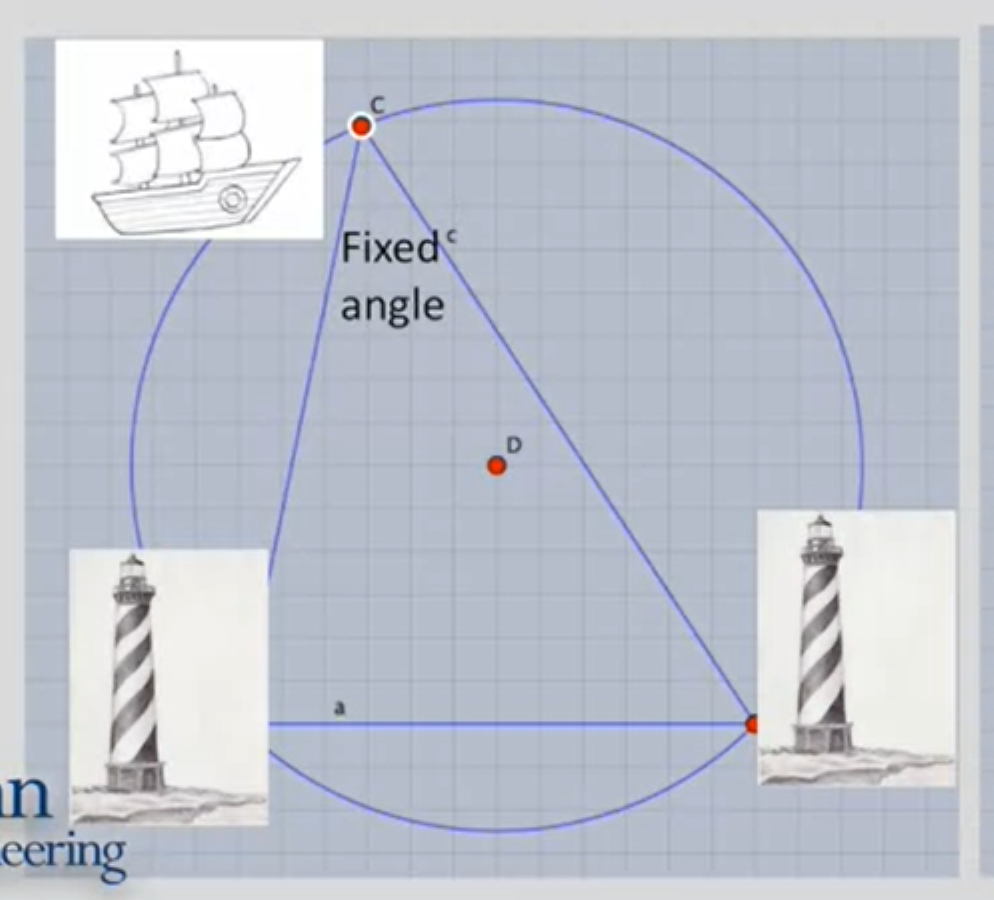
- 在3D世界中,同样已知2点的位置,相机会被越说在一个曲面内

- Tienstra公式
- 已知3点所对应的角度,可以确定观察者的位置