Robotics-Perception-week2[2]
Two Method Of Perception Matrix with 4 points
线性代数推导
- 参考
- inf.ed.ac.uk
- [多视图几何 2.3]
- 对于点$x$经过$H$变换后有如下公式 $\begin{aligned} \begin{bmatrix} y'\\x'\\1 \end{bmatrix} &= \mathbf{H} \begin{bmatrix} x\\y\\1 \end{bmatrix}\\ &= \begin{bmatrix} h_{11}&h_{12}&h_{13}\\ h_{21}&h_{22}&h_{23}\\ h_{31}&h_{32}&h_{33} \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix}\\ \end{aligned}$
- 根据一个点，我们可以得到两个方程组 $\begin{aligned} x' &= \frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\ y' &= \frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}\\ \end{aligned}$
- 其中$h_{31}x+h_{32}y+h_{33}$ 用于表示一个未知的倍数变量
- 表示成矩阵形式有 $\begin{bmatrix} x&y&1&0&0&0&-x'x&-x'y&-x'\\ 0&0&0&x&y&1&-y'x&-y'y&-y'\\ \end{bmatrix} \begin{bmatrix} h_{11}\\ h_{12}\\ h_{13}\\ h_{21}\\ h_{22}\\ h_{23}\\ h_{31}\\ h_{32}\\ h_{33}\\ \end{bmatrix}=0$
- 4点联立，有 $\begin{bmatrix} x_1&y_1&1&0&0&0&-x_1'x_1&-x_1'y_1&-x_1'\\ 0&0&0&x_1&y_1&1&-y_1'x_1&-y_1'y_1&-y_1'\\ x_2&y_2&1&0&0&0&-x_2'x_2&-x_2'y_2&-x_2'\\ 0&0&0&x_2&y_2&1&-y_2'x_2&-y_2'y_2&-y_2'\\ x_3&y_3&1&0&0&0&-x_3'x_3&-x_3'y_3&-x_3'\\ 0&0&0&x_3&y_3&1&-y_3'x_3&-y_3'y_3&-y_3'\\ x_4&y_4&1&0&0&0&-x_4'x_4&-x_4'y_4&-x_4'\\ 0&0&0&x_4&y_4&1&-y_4'x_4&-y_4'y_4&-y_4'\\ \end{bmatrix} \begin{bmatrix} h_{11}\\ h_{12}\\ h_{13}\\ h_{21}\\ h_{22}\\ h_{23}\\ h_{31}\\ h_{32}\\ h_{33}\\ \end{bmatrix}=0$
- 当左侧矩阵可逆时，方程又解，令$h_3$为1，求解其他$h$
构造基向量
- 我们需要求映射$H$, 使得$\mathbf{Ha=a’},\dotsc, \mathbf{Hd=d’}$
- 由于$\mathbf{a,b,c}$三点线性无关，因此，总可以找到一种比例$\alpha, \beta, \gamma$ 使得$\alpha \mathbf{a} + \beta \mathbf{b} + \gamma \mathbf{c} = \mathbf{d}$
- 写成矩阵形式为 $A\begin{bmatrix} 1\\1\\1 \end{bmatrix} =\begin{bmatrix} \alpha \mathbf{a}&\beta \mathbf{b}&\gamma \mathbf{c} \end{bmatrix} \begin{bmatrix} 1\\1\\1 \end{bmatrix} =d$
- 同理, 由于空间不变性，在射影空间中，$\mathbf{a’,b’,c’}$依然线性无关 $B\begin{bmatrix} 1\\1\\1 \end{bmatrix} = \begin{bmatrix} \alpha' \mathbf{a'}&\beta' \mathbf{b'}&\gamma' \mathbf{c'} \end{bmatrix} \begin{bmatrix} 1\\1\\1 \end{bmatrix} =\mathbf{d'}$
- 那么我们可以变换一下，有 $\begin{aligned} &\begin{bmatrix} 1\\1\\1 \end{bmatrix} =\mathbf{A^{-1}d=B^{-1}d'}\\ &\mathbf{BA^{-1}d=d'}\\ &\mathbf{Hd=d'} \end{aligned}$
- $\mathbf{H=BA^{-1}}$即为所求矩阵
计算例子(1)
$\begin{matrix} (1,0,0)\\(0,1,0)\\(0,0,0)\\(1,1,1) \end{matrix} \rightarrow \begin{matrix} (1,0,0)\\(0,1,0)\\(0,0,0)\\(2,1,1) \end{matrix}$ $M=\begin{bmatrix} 2&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}$
计算例子(2)
$\begin{matrix} (0,0,1)\\(1,1,1)\\(1,0,1)\\(0,1,1) \end{matrix} \rightarrow \begin{matrix} (0,0,1)\\(1,1,1)\\(1,0,0)\\(0,1,0) \end{matrix}$ $A=\begin{bmatrix} -1&0&0\\ 0&-1&0\\ -1&-1&1 \end{bmatrix}$
计算例子(3)
$$
\begin{matrix}
(1,0,0)\\(0,1,0)\\(0,0,1)\\(1,1,1)
\end{matrix}
\rightarrow
\begin{matrix}
(-2,0,1)\\(0,1,-1)\\(-1,2,-1)\\(-1,1,1)
\end{matrix}
$$
$$
A=\begin{bmatrix}
-\frac{2}{3}&0&1\\
0&\frac{5}{3}&-2\\
\frac{1}{3}&-\frac{5}{3}&1
\end{bmatrix}
$$
Cross-ratio[交比定理]
CR = lambda ac,ad,bc,bd: ac*bd/bc/ad
- 定义: Cross-ratio ${A,B;C,D}=\frac{AC}{AD}:\frac{BC}{BD}$
- 有${A,B;C,D} = {A’,B’;C’,D’}$
- 性质
- 影射[Perception transform]不变性
- 利用三角形面积证明
$$
\begin{aligned}
\{A,B;C,D\}&=\frac{AC}{AD}:\frac{BC}{BD}\\
&=\frac{AC·BD}{AD·BC}\\
&=\frac{S_{\triangle ACO}·S_{\triangle BDO}}{S_{\triangle ADO}·S_{\triangle BCO}}\\
&=\frac{AO·CO\sin(\angle AOC)·BO·DO\sin(\angle BOD)}{AO·DO\sin(\angle AOD)·BO·CO\sin(\angle BOC)}\\
&=\frac{\sin(\angle AOC)\sin(\angle BOD)}{\sin(\angle AOD)\sin(\angle BOC)}
\end{aligned}
$$
- 因此，交比只与角度有关，因此是定值
利用交比定理计算
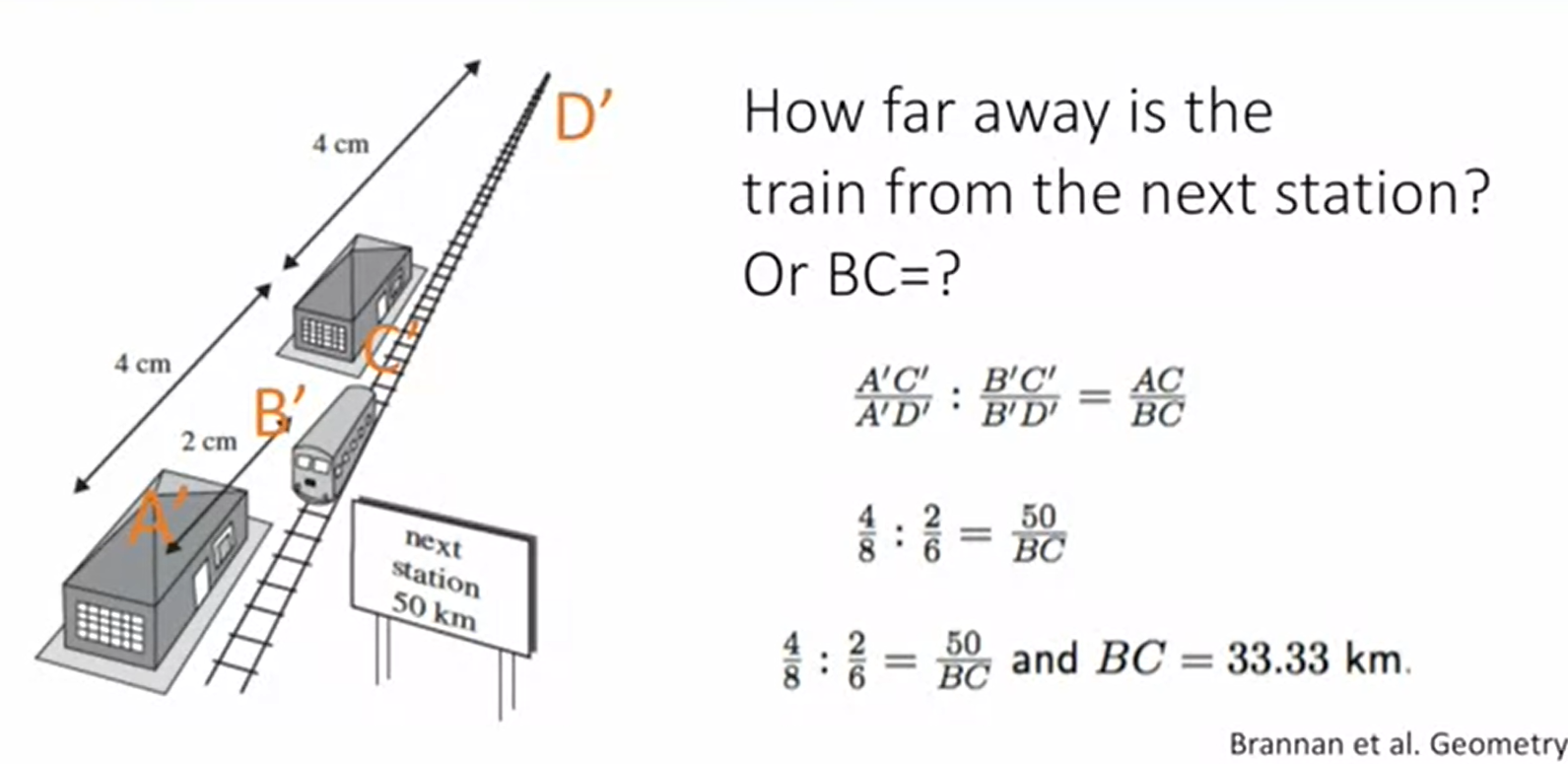
- 求解火车到下一个火车站的距离
- 由图知，$A’B’=2,A’C’=4,C’D’=4$
- 有${A’,B’;C’,D’}=\frac{A’C’}{A’D’}:\frac{B’C’}{B’D’}=\frac{1}{6}$
- 已知$AC=50km$, from image
next station 50km - ${A’,B’;C’,D’}={A,B;C,D}=\frac{AC}{BC}$, 由于D点在无穷远，因此，$\frac{AD}{BD}\simeq1$
- $BC=33.33km$
寻找灭点[Vanishing point]
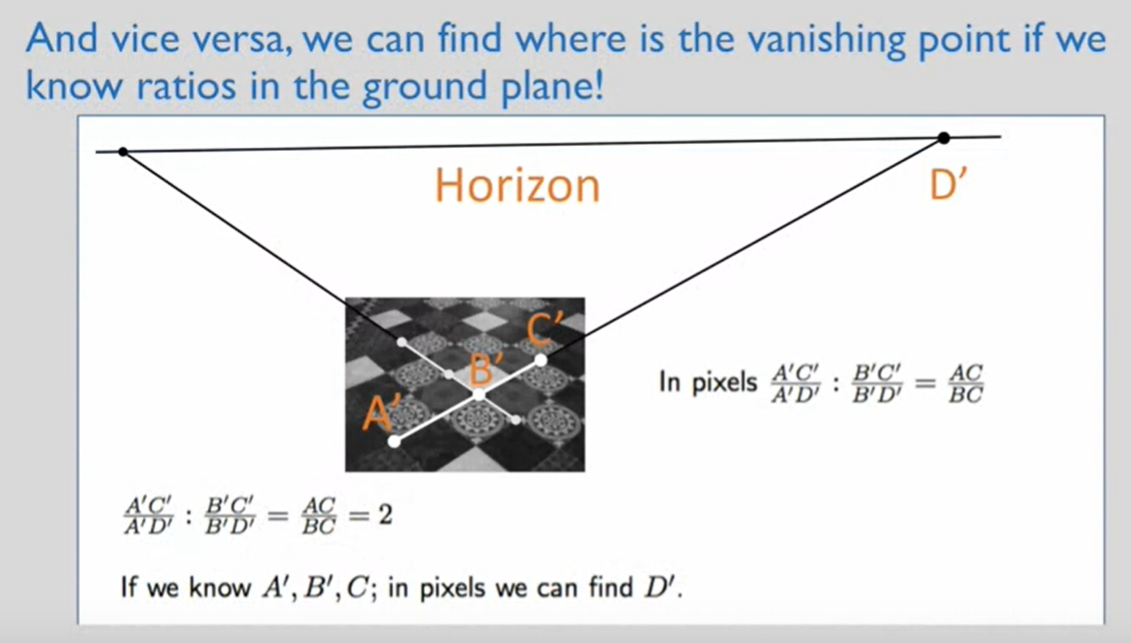
- 求解灭点D在图像中的位置
- 根据图片，有$\frac{A’C’}{A’D’}:\frac{B’C’}{B’D’}=\frac{AC}{BC}$
- 因为是瓷砖
- 所以$\frac{AC}{BC}=2$
- 那么如果已知$A’,C’,D’$的位置，即可计算出$D’$的位置
