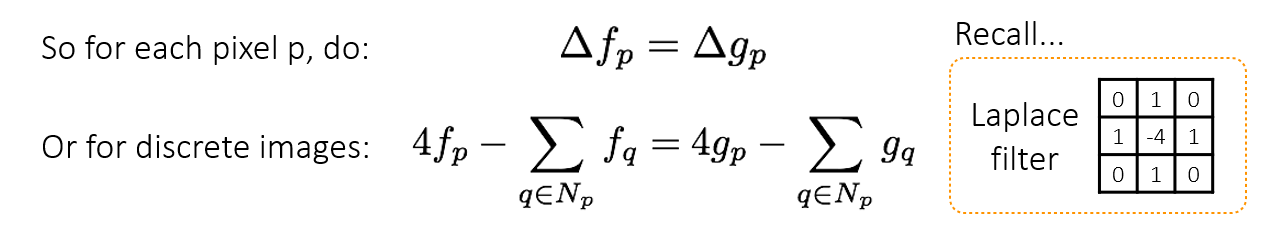Python
output = cv2.seamlessClone(src, dst, mask, center, flags)
Definitions

- $g$: 原始图像,左图企鹅
- $f$: 插值函数
- $f^*$: 目标图像
- $\Omega$: 目标域
- $\partial\Omega$: 目标域边缘,边界
Basic idea
- 期望的结果
- 填补内容要尽可以平滑
- 填补内容的边界像素值和现有的$S$一致,即要无缝过度
- 变分方程
- $\underset{f}{\min}\iint_\Omega\vert\nabla f\vert^2$ with $f\vert_{\partial\Omega}=f^*\vert_{\partial\Omega}$
- E-L Equation
- $\Delta f=0$ over $\Omega$ with $f\vert_{\partial\Omega}=f^*\vert_{\partial\Omega}$
- $\Delta$: 二阶微分, 散度divergence
- $f\vert_{\partial\Omega}=f^*\vert_{\partial\Omega}$: Dirichlet boundary: 给出边界处函数在边界处的实际值.
- Neumann boundary: 给出函数在边界处的二阶导数值
guidance vector field[引导向量场]
- 期望的结果
- 填补内容的梯度要尽可以与$\mathbf{v}$接近
- 填补内容的边界像素值和现有的$S$一致,即要无缝过度
- 变分方程
- $\underset{f}{\min}\iint_\Omega\vert\nabla f-\mathbf{v}\vert^2$ with $f\vert_{\partial\Omega}=f^*\vert_{\partial\Omega}$
- E-L Equation
- $\Delta f=div(\mathbf{v})$ over $\Omega$ with $f\vert_{\partial\Omega}=f^*\vert_{\partial\Omega}$
- $\Delta f=\frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2}$: Laplacian
- $div(\mathbf{v}) = \frac{\partial u}{\partial x} + \frac{\partial u}{\partial y}=\frac{\partial^2g}{\partial x^2}+\frac{\partial^2g}{\partial y^2} = \Delta g$: Divergence[散度]
- $\mathbf{v}=\nabla g$: Gradient[梯度]
discrete algorithm
算法变种
- Seamless Cloning[无缝克隆], 泊松编辑
- Mixing Gradients Seamless Cloning
- for all $x\in \Omega , \mathbf{v(x)}=\begin{cases}\nabla f^(\mathbf{x})&\vert\nabla f^(\mathbf{x})\vert\gt\vert\nabla g(\mathbf{x})\vert
\nabla g(\mathbf{x})&otherwise\end{cases}$
- Seamless Cloning
- Mixing Gradients Seamless Cloning
- Texture flattening
- for all $x\in \Omega , \mathbf{v(x)}=M(\mathbf{x})\nabla f^*(\mathbf{x})$
grad(abs(grad)<0.08)=0;
grad(abs(grad)<0.02)=0;
- Local illumination changes
- Local color changes
- Using three channel

- Seamless tiling
Additional reading
Reference