PID and laplace transform
PID Control
- 最常见的形式
- $u(t)=K_pe(t)+K_i\int_0^te(\tau)d\tau+K_d\frac{d}{dt}e(t)$
- 其中
- $K_p$为比例(proportional)增益
- $K_i$为积分(integral)增益
- $K_d$为微分(derivative)增益
- $e=SP-PV$为误差,设定值(setpoint)$SP$与过程值(process variable)$PV$的差
- $t$为时间
- $\tau$积分变数,因为是历史状态的积分,因此要与$t$区分开来
比较常见的解释和应用
- 通过控制水箱的流入速度,使得水箱内的高度或体积保持不变的一种过程
- 汽车定速巡航,遇到上坡如何设计动力
- 无人机的悬停和应激相应(推一下回到原来的位置,或者前往目标点)
- 解决电路问题
PID
- 通常学习PID控制时,往往不太懂得3个变量的实际作用,又有计算机作为辅助进行模拟,那么就会导致盲目调参,而书中提到的调参方法又只讲参数含义,将调参性质描述一遍,这样完全不得法门,最后只能得到一个差不多的结果
- 历史上
- 惠更斯17世纪改造了风车,使得磨盘转速和磨盘间隙可以根据谷物数量变化
- Power From the Wind , Cambridge University Press
- 瓦特使用圆锥摆以解决蒸汽机的速度输出
- 1868年,为了更好的保持鱼雷的深度,引入了微分控制
- 直到1922年,才有了完整的3项控制率
- 惠更斯17世纪改造了风车,使得磨盘转速和磨盘间隙可以根据谷物数量变化
- 因此,大多数书籍往往会根据每项变量引入时发挥的作用加以解释,但是又与纯PI控制,PD控制,甚至单纯的P控制应用相违背,除了硬件或成本上的限制,更需要思考的是,每一项为整个系统的稳定性到底提供了多大的好处
PID调参
- 为了获得更好的参数,有如下几种方法
- 手动
- Ziegler–Nichols[齐格勒-尼科尔斯方法]
- Ziegler–Nichols_method - Wikipedia
- 使用Z-N方法调节气压 - Bilibili
- 将ID项置0,调节P使得达到恒定震荡,再根据震荡周期和震荡值计算PID参数
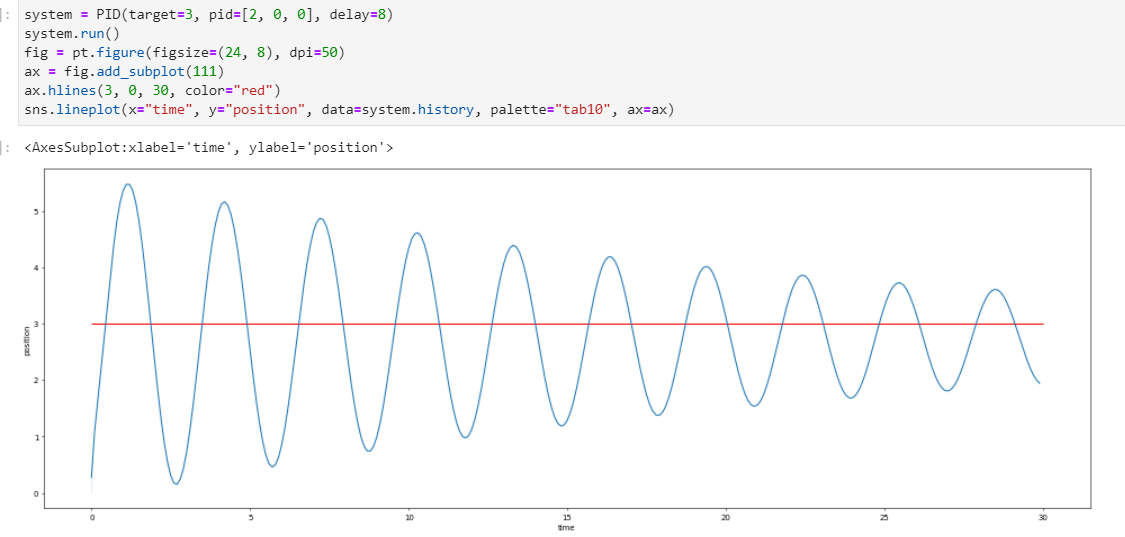
- 注意,想要在P控制下得到稳定震荡,要有超调现象,如果通过计算机模拟,而时间单位又很小,那么无论用多大的$K_P$你都看不到超调现象,可以理解为,系统刚刚输入一点点就被感知到了,而上面视频里从气流输入到输出存在一定的延迟,因此可以使用该方法
- 反馈较慢
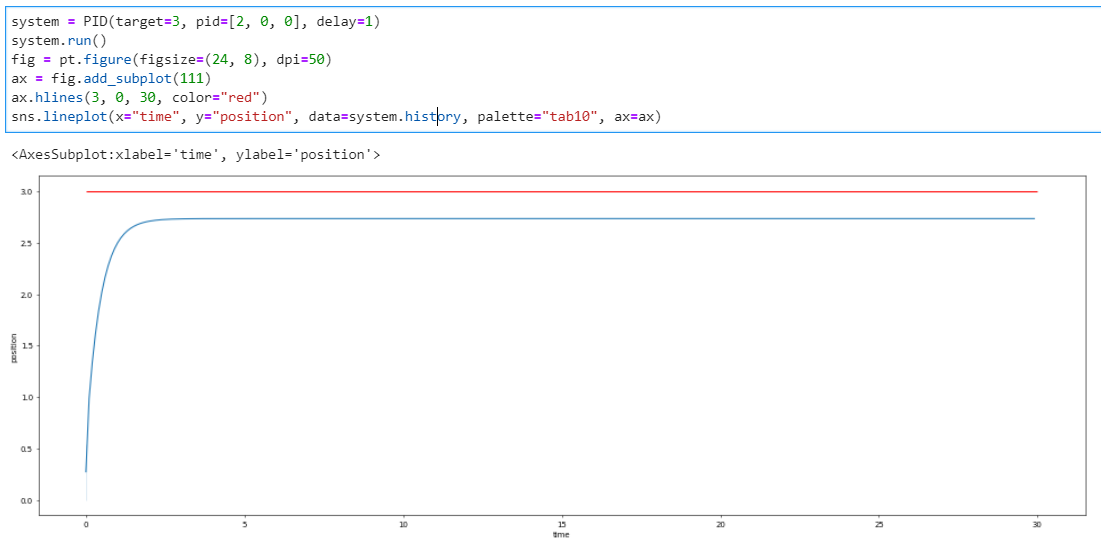
- 快速反馈
- 两处代码只更改了延迟
- 机器学习[反向传播]
- 今天聊聊PID - zzzSid的文章 - 知乎
- 目标函数$cost = \frac{1}{2}(position_t-target_t)^2$
- 不过我并不是很赞同他使用动态参数的做法
- 目标函数也未考虑收敛速度和周期
- 基于支持向量机回归和RBF神经网络的PID整定 - 海军航空工程学院
- 原理跟上面一样
- 今天聊聊PID - zzzSid的文章 - 知乎
理论分析
Laplace Transform[拉普拉斯变换]
- 其中$s$是个复数
- 为了更好的理解Laplace Transform, 回想一下Fourier transform[傅里叶变换]
- $F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt$, $i$是虚数单位
- 同时它也有另外一种表示
- $F(\omega) = \int_{-\infty}^{\infty}f(t)*\sin(\omega t)dt$
- 这是因为欧拉公式可以建立起复数和三角函数之间的关系
- 傅里叶变换和拉普拉斯变换的主要区别
- 傅里叶变换的积分域为$(-\infty,+\infty)$, 而拉普拉斯变换的积分区间为$(0, +\infty)$
- 由于傅里叶变换主要关心函数的周期性,频率性质,而这些性质需要假设函数拥有周期或者周期无限长,对于一些01信号也需要利用周期函数的性质再将其进行延拓
- 而拉普拉斯变换主要解决应用问题,$t$常常作为时间表示,而时间没有负值,因此拉普拉斯变换常常不考虑负值的情况,不过依然存在双边拉普拉斯变换的情形bilateral Laplace transform
- Why does Laplace transform take the integral with limit beginning at zero - Quora
- 傅里叶变换使用纯虚数,而拉普拉斯变换将其扩大到了整个复数域
- 这里有三种理解方式
- 将$s$分离成实数和虚数两个部分
- $L(s)=\int_0^{\infty}f(t)e^{-i\omega t}e^{-\sigma t}dt$
- 其中$\omega, \sigma$都为实数
- 这样拉普拉斯变换就只是在傅里叶的基础上乘了$e^{-\sigma t}$
- 这样就解决了一些非周期的以及$f\to\infty$区域无穷的函数利用傅里叶不可积的问题
- 当然如果存在$f$比$e^{\sigma t}$的增长速度还要快的函数,那么拉普拉斯变换也依然存在不可积的问题
- 将这两种变换理解为函数值之间的内积或者卷积
- 为了得到一些频率的信号量,我们选择一组正交基,比如一些三角函数,我们用$f(t)·e^{-i\omega t}$(它是傅里叶变换的内积形式),找到在该周期内最大的响应,然后依次求出各个周期的信号大小,这就是傅里叶级数的求法
- 同时,为了解决傅里叶级数需要周期无限长的问题,也有Wavelet transform[小波变换], 等
- 如果不考虑基的正交性,你还可以自己设计一个新的函数
- 例如在图像领域的Box-Filter[盒子滤波器], 它仅仅是二维高斯函数的离散化点阵而已,用以加快计算速度,或者其他CNN中所用的filter,也是同样的作用
- 那么这时,拉普拉斯变换中$e^{-i\omega t}e^{-\sigma t}$就变成了一个幅度不断增长或下降的三角函数,我们通过它就可以知道一个函数的指数收敛性,或者发散速度
- 第三种将其理解为一种在复数空间中的投影
- 将$s$分离成实数和虚数两个部分
- Reference
- 这里有三种理解方式
- 傅里叶变换的积分域为$(-\infty,+\infty)$, 而拉普拉斯变换的积分区间为$(0, +\infty)$
- 计算例子
-
$$ \begin{aligned} L(s)=\mathcal{L\{f(t)\}} &= \int_{0^{-}}^\infty f(t)e^{-st}dt\\ &=\left[\frac{f(t)e^{-st}}{-s}\right]_{0^{-}}^\infty-\int_{0^{-}}^\infty\frac{e^{-st}}{-s}f'(t)dt&(1)\\ &=\left[0-\frac{f(0^{-})}{-s}\right] + \frac{1}{s}\mathcal{L\{f'(t)\}}\\ \mathcal{L\{f'(t)\}}&=s\mathcal{L\{f(t)\}}-f'(0^{-})\\ \mathcal{L\{f'(t)\}}&=sL(s)-f'(0^{-})\\ \end{aligned} $$
- 其中
-
$(1)$使用了分部积分法,同时使用了隐含条件$\lim\limits_{t\to \infty} f(x)e^{-st} = 0$, 即前文提到的,$f(t)$的增长速度没有$e^{st}$快,因此作为分母时才可以使得$f(x)e^{-st} _{t=\infty}=0$ - $0^{-}$的解释
-
Wikipedia 这个极限强调任何位于 0 的质点都被拉普拉斯变换完全捕获。虽然在使用勒贝格积分时,我们没有必要取这个极限,但它让我们更自然地与拉普拉斯–斯蒂尔吉斯变换建立联系。
-
- 其中
-
- 比较常用的其他例子
-
$$ \begin{aligned} \mathcal{L\{tf(t)\}}&= \int_{0}^\infty tf(t)e^{-st}dt\\ &=\int_{0}^\infty [te^{-st}]f(t)dt\\ &=\int_{0}^\infty -[-te^{-st}]f(t)dt\\ &=\int_{0}^\infty -[\frac{d}{ds}e^{-st}]f(t)dt\\ &=-\frac{d}{ds}\int_{0}^\infty f(t)e^{-st}dt&(1)\\ &=-L'(s) \end{aligned} $$
- 其中
- $(1)$利用了积分和求导的顺序交换不变性
- 延伸阅读
- 其中
- 二阶导
-
$$ \mathcal{L\{f''(t)\}}=s^2L(s)-sf(0^{-})-f'(0^{-}) $$
-
- 积分
-
$$ \int_0^tf(\tau)d\tau=\frac{1}{s}L(s) $$
-
- MIT—微分方程笔记20 拉氏变换求解线性常微分方程 - 三少爷的键的文章 - 知乎
- 拉普拉斯(Laplace)变换在广义积分求值中的应用 - fell的文章 - 知乎
-