A kind of mind for 3d manifold to 2d

问题，希望建立一种2d坐标对应3维流形坐标的方法

• 类似问题：
  • 1维方程$R_1\rightarrow R_1$, 可以使用参数方程进行0,1映射
  • 点集，可以使用ICP进行匹配，但可能会造成过拟合

$R_2\rightarrow R_3$

数据是空间点云

方案1，以点的路径和作为极坐标的距离，以投影方向作为极坐标的角度

• 投影方向可以使用PCA，即所有点距离初始点的方差最大的方向作为投影面法线
• 距离使用树的路径积分
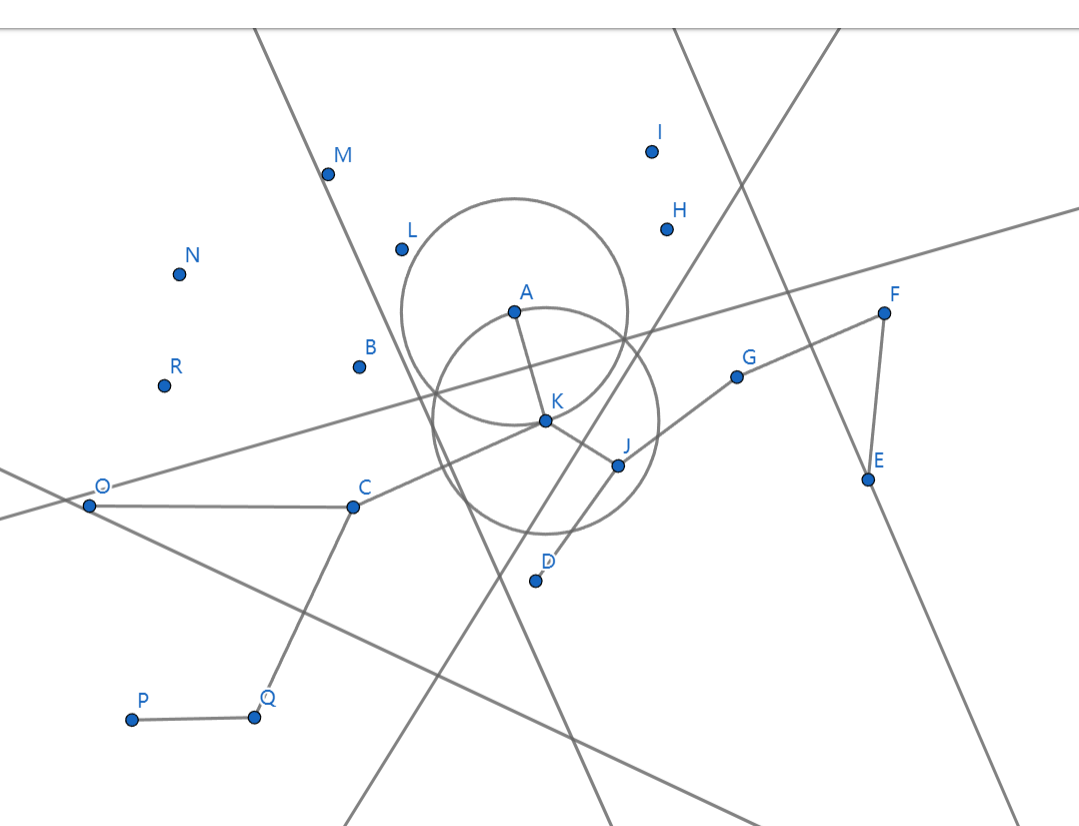
  • 如图所示，以A为原点，最近点为K，AK做垂直平分线(或面)，K侧的点不在作为A的子树，因为他们距离k的距离都小于A，可以通过二分查找进行优化
  • 距离k最近的点为J，此时KJ的垂直平分线划分出的COQP点只属于K的子树，因为他们距离K的距离都小于J
  • 此时，A到C的距离为，AK+KC
  • 尽管AC距离更短，但由于KC短于AC，因此C更适合作为K的后继
  • 当采样点足够多时，若ACK在同一平面，则AC约等于AK+CK，若ACK不在同一平面，则AK+CK更适合表示AC的距离

Reference

• 做图工具
  • https://www.geogebra.org/geometry
• 清华笔记：计算共形几何讲义 （16）拓扑球面的调和映照
• B样条曲面和曲线