Trangle Rasterization
OpenMVS[Homogeneous Coordinate]
Line sweeping[线扫法]
- Triangle-rasterization-and-back-face-culling
- 对y排序,从左向右设置像素
- 分两段画完
Barycentric Coordinates[重心坐标系判定法 - 并行计算中的判定]
- 遍历AABB内的所有点的重心坐标
- For Convex
- 重心坐标具有仿射不变性
- As Area coordinates in trangle
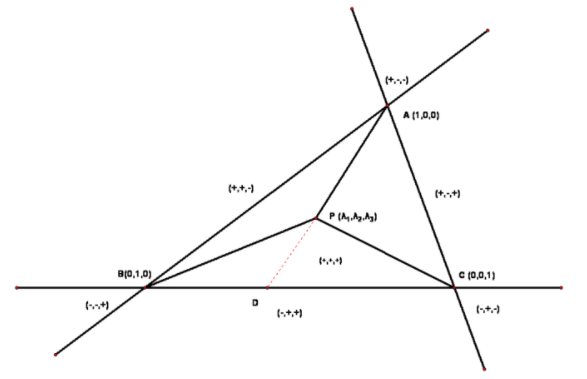
- 对于三点$A,B,C$的坐标分别为$\mathbf{a,b,c}$
- 对于任意点$P$的坐标$p$
- 设$S_{\triangle{PBC}}:S_{\triangle{PBC}}:S_{\triangle{PBC}}=\lambda_1:\lambda_2:\lambda_3$
- $\lambda_1+\lambda_2+\lambda_3=1$
- 延长$AP$交$BC$于$D$
-
$$ \begin{aligned} &\because&BD:DC&=\lambda_3:\lambda_2\\ &\therefore& \mathbf{d}&=\frac{\lambda_2\mathbf{b}+\lambda_3\mathbf{c}}{\lambda_2+\lambda_3}\\ &\because&AP:PD&=(\lambda_2+\lambda_3):\lambda_1\\ &\therefore&\mathbf{p}&=\frac{(\lambda_2+\lambda_3)\mathbf{d}+\lambda_1\mathbf{a}}{\lambda_1+\lambda_2+\lambda_3}\\ &\therefore&\mathbf{p}&=\lambda_1\mathbf{a}+\lambda_2\mathbf{b}+\lambda_3\mathbf{c} \end{aligned} $$
- 因此,重心坐标, 也是面积坐标
-
For each pixel we compute its barycentric coordinates. If it has at least one negative component, then the pixel is outside of the triangle.
- 点在三角形内的问题转换为求解重心坐标
- 面积法
-
$$ \lambda_1=\frac{S_{\triangle{PBC}}}{S_{\triangle{ABC}}}=\frac{\begin{vmatrix} 1&x_p&y_p\\ 1&x_b&y_b\\ 1&x_c&y_c\\ \end{vmatrix}}{\begin{vmatrix} 1&x_a&y_a\\ 1&x_b&y_b\\ 1&x_c&y_c\\ \end{vmatrix}} $$
- 其中
-
$$ S_{\triangle_{ABC}}=\frac{1}{2}\begin{vmatrix} 1&x_a&y_a\\ 1&x_b&y_b\\ 1&x_c&y_c\\ \end{vmatrix} $$
-
- 代数法
-
$$ \begin{cases} \lambda_1x_a+\lambda_2x_b+\lambda_3x_c&=x_p\\ \lambda_1y_a+\lambda_2y_b+\lambda_3y_c&=y_p\\ \lambda_1+\lambda_2+\lambda_3&=1\\ \end{cases} $$
-
- 面积法
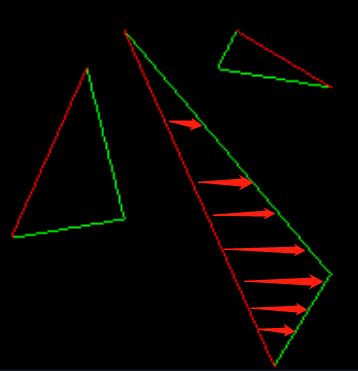
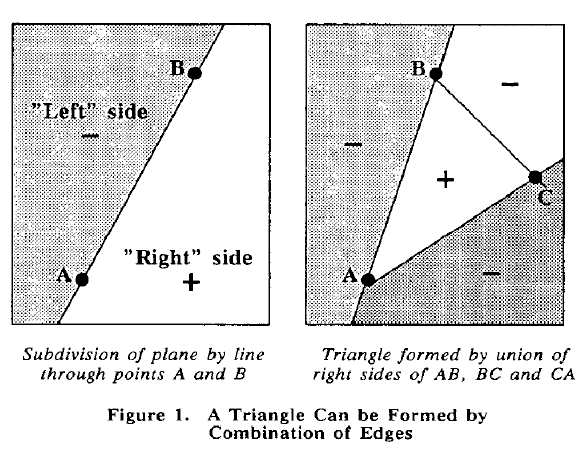
Linear Edge Function, Line sweeping[线边法]
- A parallel algorithm for polygon rasterization
- Paper.pdf
- 主要描述线扫法和并行计算中对多边形的填充设计
-
$$ \begin{aligned} dX_i &= X_i - X_{i-1}\\ dY_i &= Y_i - Y_{i-1}\\ E_i(X, Y) &= (X-X_i)dX_i - (Y-Y_i)dY_i \end{aligned} $$
- 多边形内为正,多边形外为负,线上为0
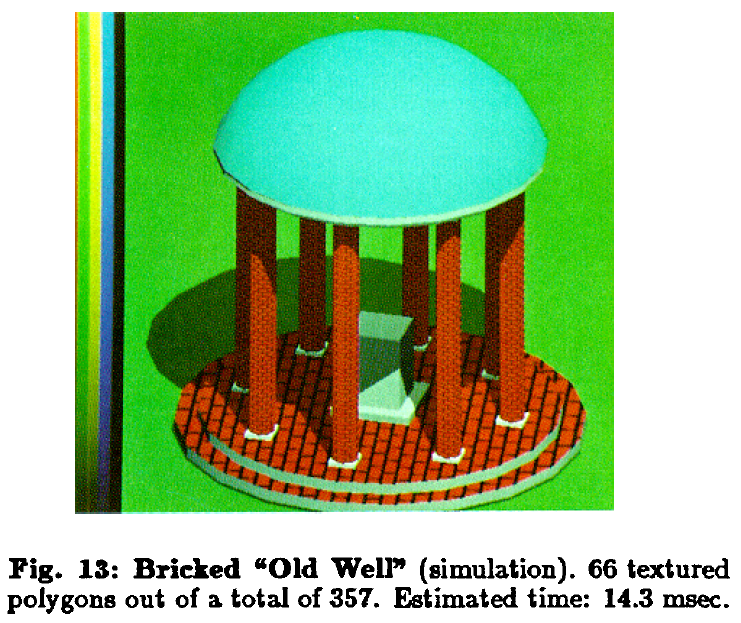
- Fast Spheres, Shadows, Textures, Transparencies, and Image Enhancements in Pixel-Planes
- 主要描述硬件渲染技术