Texture Paper Reading - [Rethinking Texture Mapping]
Rethinking Texture Mapping - State of The Art Report
1.1 Scope
- Perfecting the Traditional Texture Mapping
- Connectivity-based Representations
- Sparse Volumetric Textures
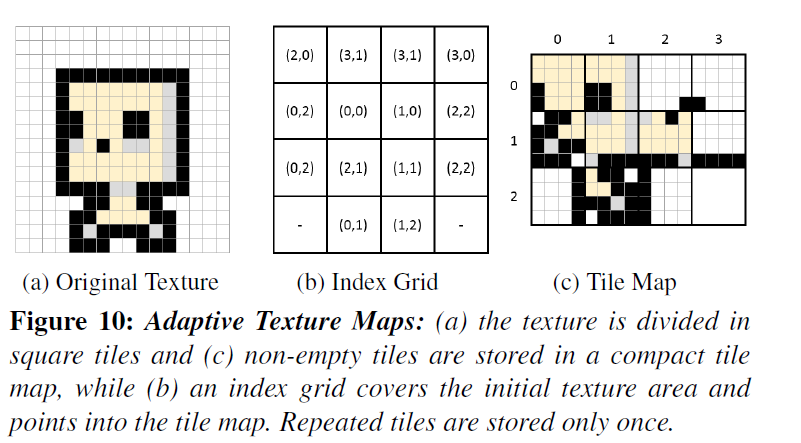
- KE02 - Adaptive Texture Maps
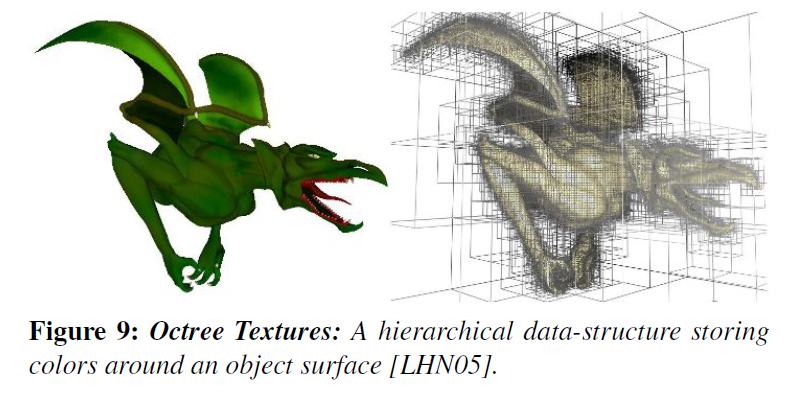
- BD02,LHN05 - Octree Textures
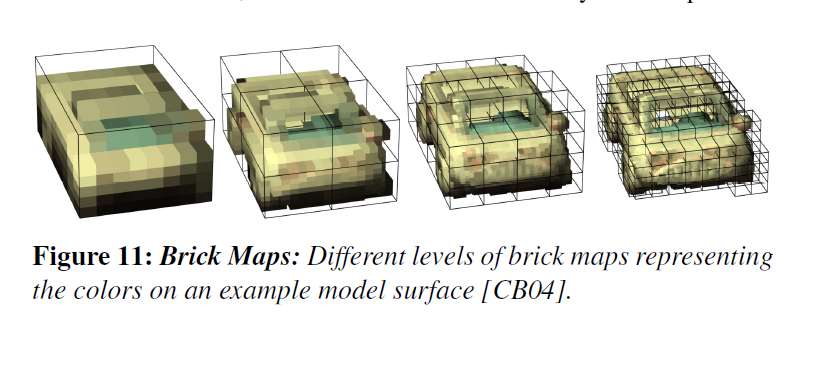
- CB04 - Brick Maps
- Perfect Spatial Hashing
- Volume-based Parameterizations
1.2 Evaluation Criteria
- Applicability.
- Usability.
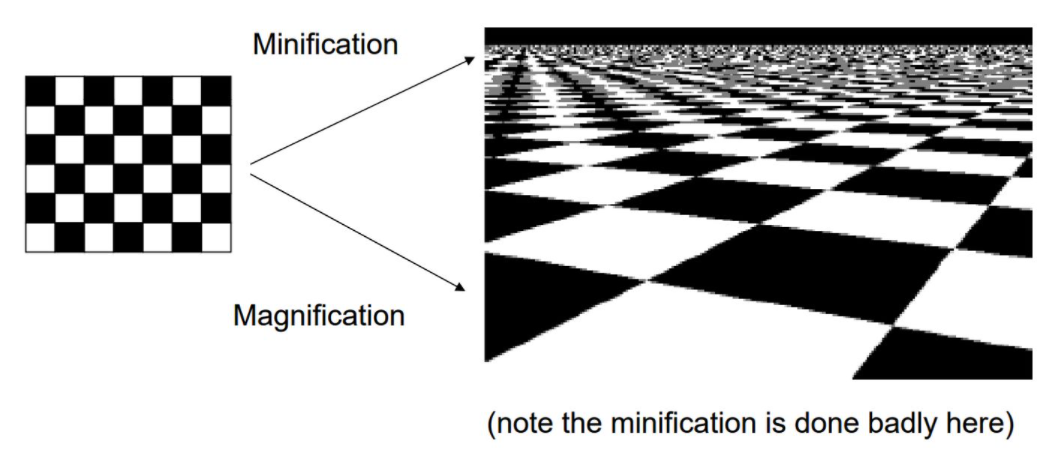
- Filtering Quality.
- magnification filtering
on-the-fly bilinear interpolation
- minification filtering
- anisotropic filtering[各向异性过滤]
- allows skewed filter shapes
- magnification filtering
- Performance.
- Implementation.
Traditional 2D Texture Mapping
assigning uv coordinates to mesh vertices
Perfecting Traditional Texture Mapping
- PKCH18 - Gradient-domain Processing Within a Texture Atlas
- Paper.pdf
- texture seams and texture distortions
- DGM18 - Generating uv maps for modified meshes - US10192346B2
- automatize the adaptations of the uv map
- SSGH01 - Texture mapping progressive meshes
- the poor interoperability of LoD-pyramids and atlas-based textures
Invisible Seams
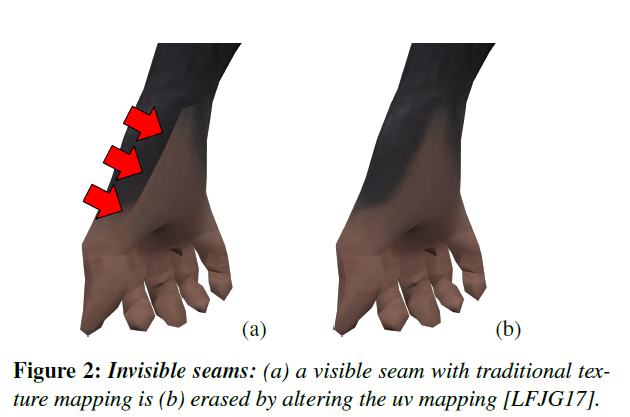
- Traditional Texture Mapping
- inconsistent bilinear filtering performed on either side of the seams
Bilinear Filtering- alias:
Bilinear Interpolation,Bilinear texture mapping -
$$ \begin{aligned} f(x, y_1) &= \frac{x_2-x}{x_2-x_1}f(Q_{11}) + \frac{x-x_1}{x_2-x_1}f(Q_{21})\\ f(x, y_2) &= \frac{x_2-x}{x_2-x_1}f(Q_{12}) + \frac{x-x_1}{x_2-x_1}f(Q_{22})\\ f(x, y) &= \frac{y_2-y}{y_2-y_1}f(x, y_1) + \frac{y-y_1}{y_2-y_1}f(x, y_2)\\ &=\frac{1}{(x_2-x_1)(y_2-y_1)}\begin{bmatrix} x_2-x&x-x_1 \end{bmatrix}\begin{bmatrix} f(Q_{11})&f(Q_{12})\\f(Q_{21})&f(Q_{22}) \end{bmatrix}\begin{bmatrix} y_2-y\\y-y_1 \end{bmatrix} \end{aligned} $$
- extension:
Trilinear interpolation
- alias:
- inconsistent bilinear filtering performed on either side of the seams
-
placing both sides of the seams axis-aligned in uv space (either horizontally or vertically) with matching lengths, and assigning texels values that are exactly replicated along the seam.
- cylindrical/toroidal mappings
- [Tar12], [THCM04]
- cylindrical/toroidal mappings
- [RNLL10]
- introduces some constraints
- integer resolution jumps across seams
-
one side of the seam to be n times the other, here $n \ge 1, n \in \mathbb{Z}$, longer side are linear interpolations of the values on the shorter side

- generating uv layouts with motorcycle graphs[SPGT18]
-
- oblique placement of seams in the 2D texture space
-
two sides of the seams are constrained to be matching in parametric space up to an integer translation and rotations by an integer multiple of $\frac{\pi}{2}$
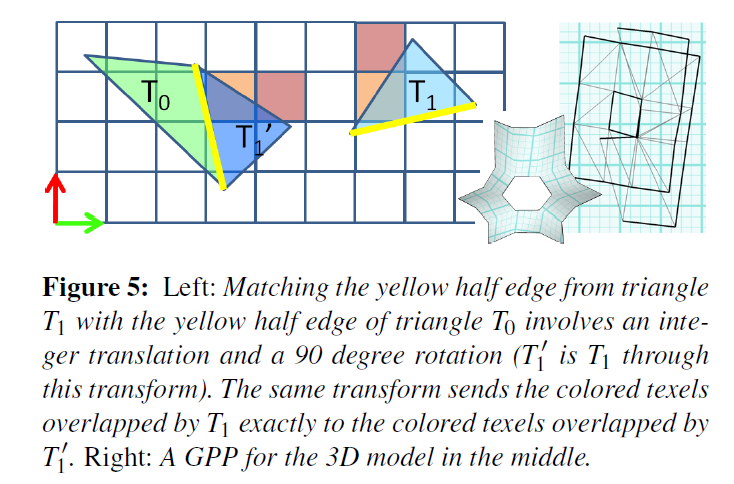
-
- integer resolution jumps across seams
- introduces some constraints
- [LFJG17] seamless cuts or erased seam
-
no constraint is explicitly imposed a priori on uv assignment
-
minimizes the discrepancy from the initial configuration
- $\underset{\min p}{E_{lerp}(e_i,x_0,x_1)}=\int_0^1\vert B(e_i(\gamma), p)-(\gamma x_0+(1-\gamma)x_1)\vert^2d\gamma$
-
minor technical note, making seams invisible (with any method) may require using texture resolutions that are powers of 2, seams can still be visible when using arbitrary texture resolutions
-
Seamless Toroidal/Cylindrical Textures
- Ignore the restriction for
only allows seams at mesh edgeswhen Toroidal/Cylindrical [Tar12] 💩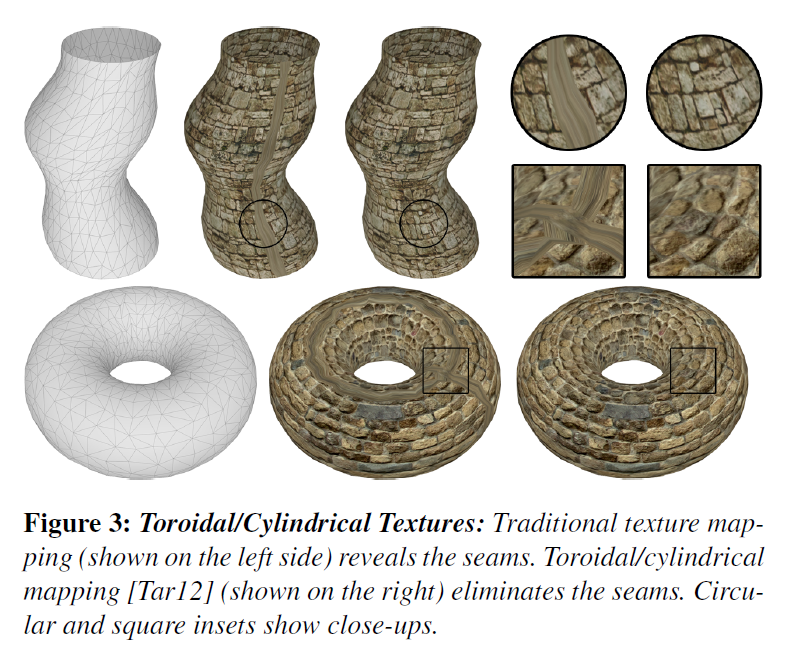
- Cylindrical -> rectangular
- Toroidal ->
two orthogonal
Seamless Texture Atlases
-
[PCK04]Mip-mapping: Texture resolutions may be selected or blended on a per-fragment basis
- Mip: multum in parvo,[放置很多东西的小空间]
- Mipmap - wiki
- Paroj - Linear Filtering


Connectivity-based Representations
- [BL08] Ptex, Disney Animation and Pixar studios
- How to
-
Since each face effectively gets its own texture, it is not affected by geometrical deformations of the model.
-
Ptex stores four face indices per face, indicating the four neighbors of each quad face
-
our edge indices are stored per face to represent which edge of each neighboring face is the shared edge
-
- resolution adjusted
-
texture resolution of each face can be adjusted independently
-
setting the texture resolution of a face based on its size.
-
texture filtering near edges becomes difficult
-
- How to
- [YKH10] Mesh colors
- Indeed, the lowest-resolution mesh colors are vertex colors, which store a single texture value per vertex

- [Yuk16] Mesh Color Textures
- GPU-friendly

Sparse Volumetric Representations
store
texture datain avoxelgrid covering the object
- Issue list
- thin surfaces get the same color on both sides
- can be alleviated by storing normals alongside colors [BD02], at the expense of a further increase in storage and lookup cost
- cost of trilinear interpolation.
- thin surfaces get the same color on both sides
- [KE02] Adaptive Texture Maps
- With traditional texture mapping, the entire texture is encoded using the same resolution, thus wasting memory where the content has low frequency.
- [BD02,DGPR02, LHN05,KLS05] Octree Textures
- [CB04] Brick Maps
- RenderMan
- [LH06]Perfect Spatial Hashing
-
This results in a very efficient method where the sparse data is accessed through only two texture lookups (a single indirection). However, the loss of cache coherency, due to the randomization of the access by the hash, penalizes access performance.

-
Volume-based Parametrizations
- how to encode the mapping efficiently and how to precompute it robustly
- [LD07]TileTrees
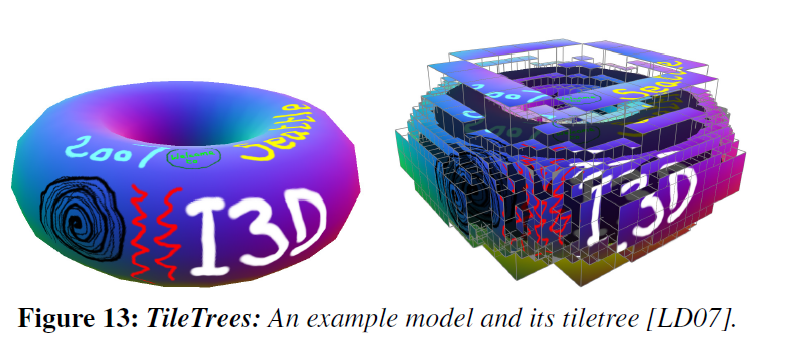
- The entire process is automatic, robust, and fast
- Tiletrees suffer from the same distortions as cube-maps
- [THCM04]PolyCube - Maps
- extension of cube-maps[Gre86]
- by substituting the cube the with an arbitrary polycube
- they replace the problem of defining a uv mapping with the problem of constructing a polycube
- The task of automatically or semi-automatically constructing a polycube-map
- [LJFW08,WJH08, HWFQ09, WYZ11, YZWL14, HJS*14, HZ16]
- limiting the number of cubes
- limiting the number of irregular vertices
- matching the topology of the input surface
- maximizing shape similarity between the two shapes
- [LJFW08,WJH08, HWFQ09, WYZ11, YZWL14, HJS*14, HZ16]

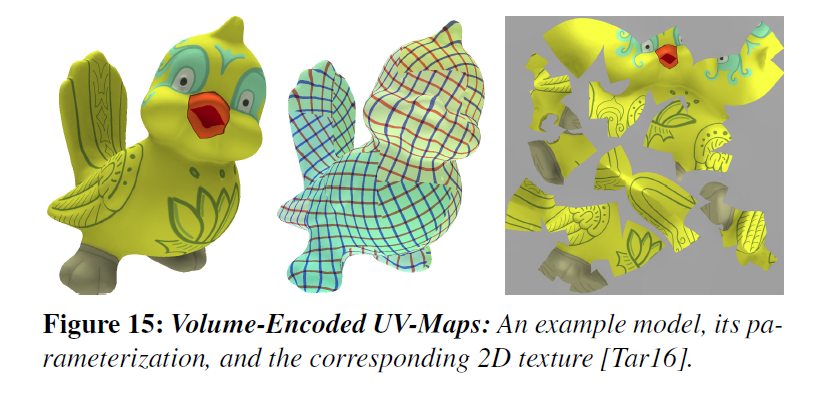
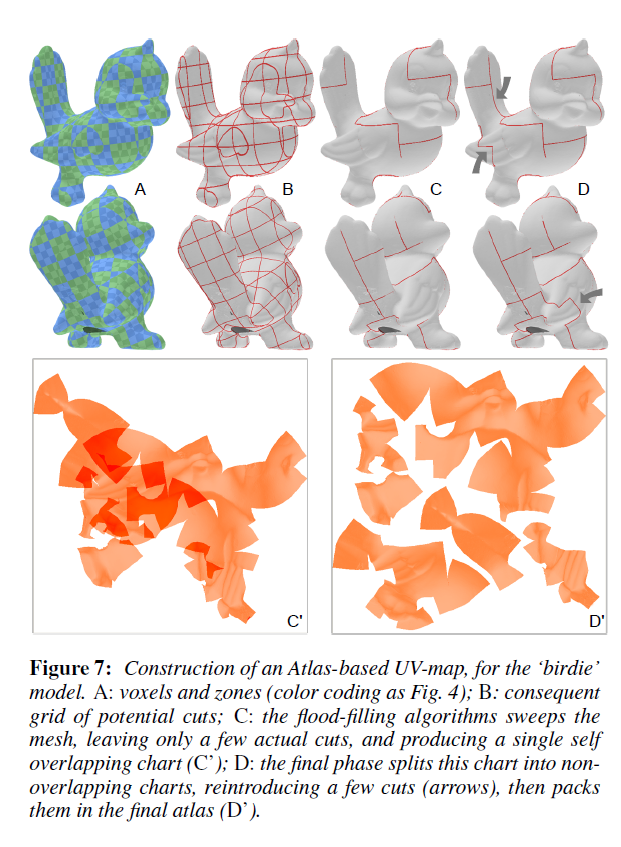
- [Tar16]Volume-Encoded UV-Maps
-
volume-encoded uv-maps replace the problem of defining a uv mapping with the problem of defining a volume-encoded parameterization
-