Point Cloud Match[2]
类局部的配准算法
- 受限于点云初始位置
- 仅适用于小角度错开的点云配准问题
- 受限于主成分分析、奇异值分解算法
- 迭代次数较多,后期收敛缓慢
- 最近邻点的成本较高,KD-tree虽然搜索效率较高,但仍无法满足于解决大规模点云的配准问题
ICP(Iterative Closest Point)
- 不断迭代原始点云的变换矩阵,直到RMSE收敛域局部最优解
- 迭代过程
- 搜索最近点集
- 构造协方差矩阵
- 奇异值分解
- 求解旋转矩阵
- OpenCv
cv2.estimateAffinePartial2D(src, dst[0, indices.T]), 4自由度cv2.estimateAffine2D(src, dst[0, indices.T]),6自由度
-
$$ \begin{cases} E(R,T)=\sum_{i=1}^N\Vert Rp_i+T-p_{closest}\Vert_2^2\\ P_{closest}=\underset{q_j}{\argmin}\Vert p_i-Q\Vert_2^2 \end{cases} $$
- 迭代过程
ICP 变种
- LM-ICP
- Moré J J. The Levenberg-Marquardt algorithm: Implementation and theory[J]. Lecture Notes in Mathematics, 1978, 630: 105-116.
- Fitzgibbon A W. Robust registration of 2D and 3D point sets. Image Vision Comput 2003;21:1145-1153.
- Levenberg-Marquardt
- Improved computation for Levenberg–Marquardt training. IEEE transactions on neural networks
- 如何用LM算法求解目标函数最小值? - Sixiang的回答 - 知乎
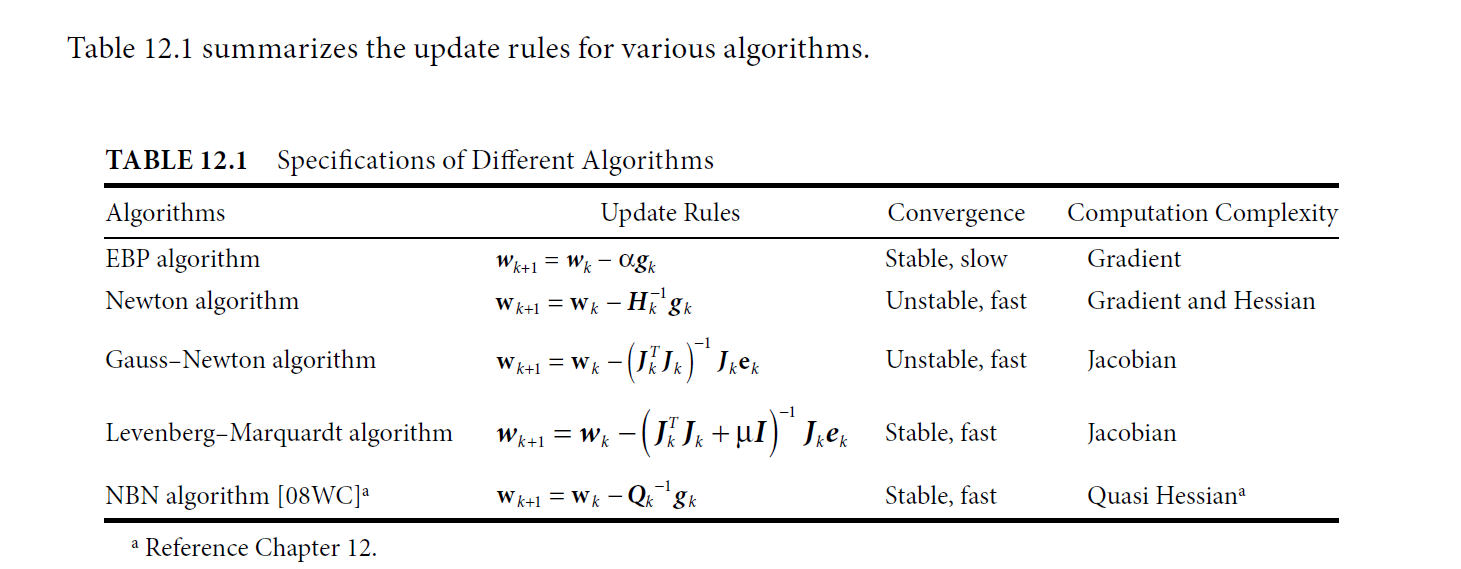
- Table 12.1
-
$$ H\approx J^TJ+\mu I $$
- $J$: Jacobian matrix
- $I$: Identity matrix
- $\mu$
- $\mu\to0$:Gauss-Newton
- $\mu\gg J$:最速下降法
- DT(Distance-Transform)替代KD-tree搜索最近邻点
- Trimmed ICP
- Chetverikov D, Svirko D, Stepanov D, et al. The Trimmed Iterative Closest Point algorithm[J], 2002.
- 筛选最近邻点
- 用欧式距离进行排序,去掉其中距离较大的点集
- Sparse ICP
- Bouaziz S, Tagliasacchi A, Pauly M. Sparse iterative closest point[C]. Eleventh Eurographics/acmsiggraph Symposium on Geometry Processing, 2013.
- 稀疏表示理论
- 范数配准模型上增加p范数的惩罚项
- 增广拉格朗日求解(效率较差)
- Efficient Sparse ICP
- Normal Distribute Transform(NDT)
- Biber P, Strasser W. The normal distributions transform: a new approach to laser scan matching[J]. Proc.of IEEE/RSJ Intl Conf.on Intelligent Robots & Systems, 2003, 3: 2743-2748 vol.3.
- 使用D维的高斯函数作为配准模型
- 源点云Q进行体素划分
- 求解点云Q的包围盒
- 包围盒进行细分
-
Magnusson
NDT算法较ICP算法能更好地避免点云初始位置对配准结果的影响
-
$$ \begin{cases} E(R,T)&=\frac{1}{(2\pi)^\frac{D}{2}\sqrt{\vert\Sigma\vert}}exp((Rp+T-u)^T\Sigma^{-1}(Rp+T-u))\\ u&=\frac{1}{M}\sum_{j=1}^Mq_j\\ \Sigma&=\frac{1}{M-1}\sum_{j=1}^M(q_j-u)(q_j-u)^T \end{cases} $$
全局的3D点云配准算法
- 启发式算法
- 需多次调用配准模型进行优化求解,在处理大规模点云配准问题时效率较低,且其全局解并未有严格的证明
- 遗传算法求解出全局优化的变换矩阵
- 粒子群算法
- 模拟退火
- 构造几何不变量匹配对应点对
- 曲率特征求解对应点对
- 构造积分体积特征计算匹配点对
- 构造点特征直方图作为局部描述符
- 4点法构造几何特征进而提取稀疏的匹配点对
- Go-ICP
- AMP
- Glob-GM-ML
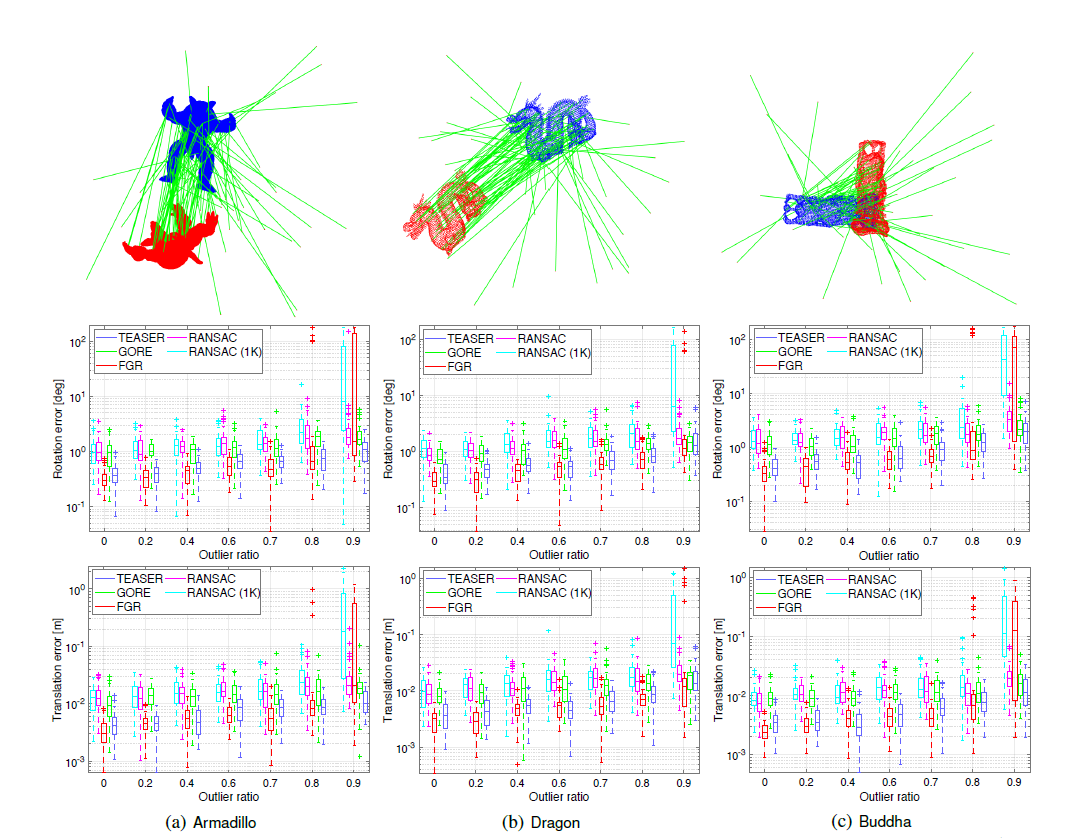
- TEASER
- GOGMA
DeepLearning Net
- 基于相似性测度研究的点云匹配
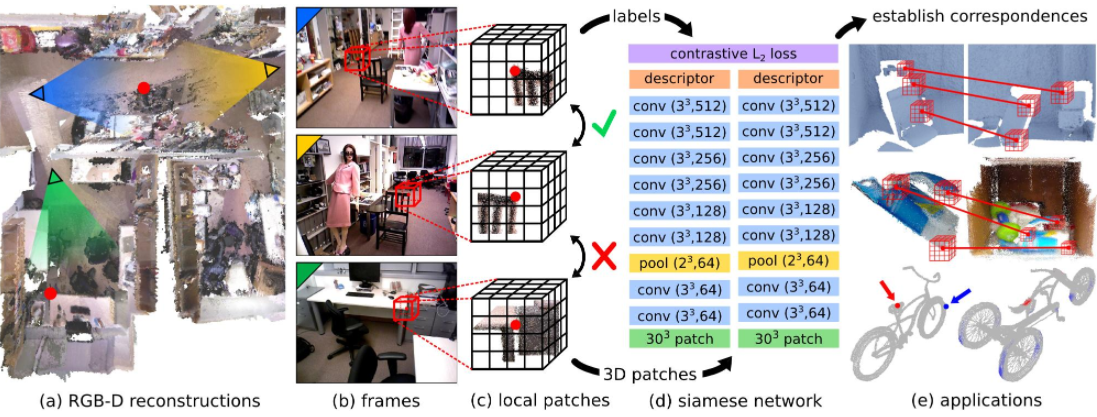
3DMatch
- Paper
- HomePage
| Repository | spark | star |
|---|---|---|
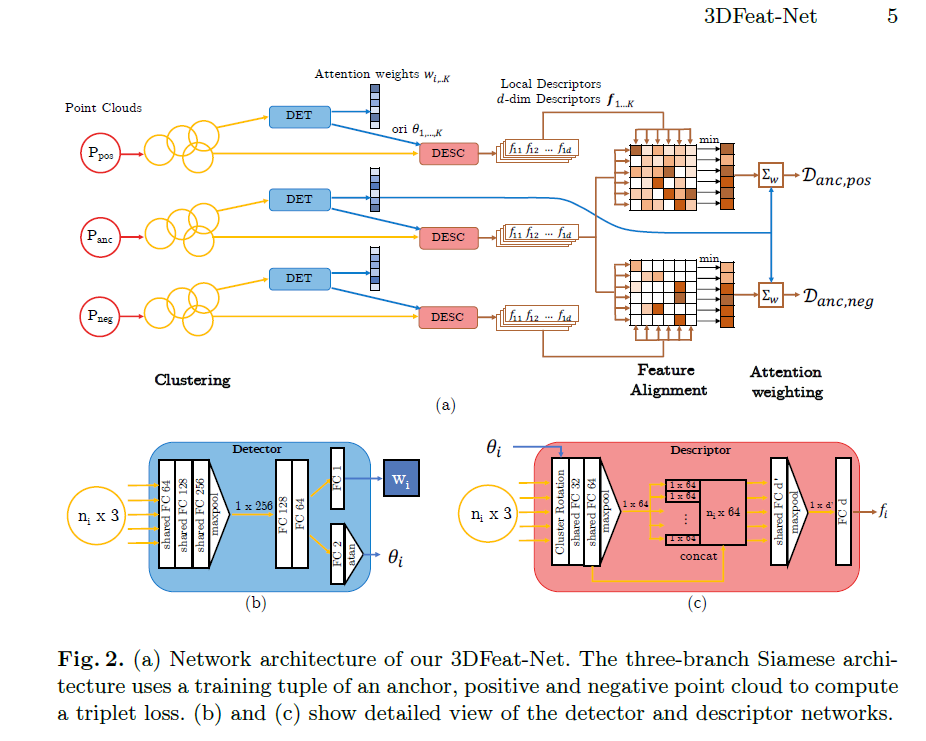
3DFeat-Net
| Repository | spark | star |
|---|---|---|
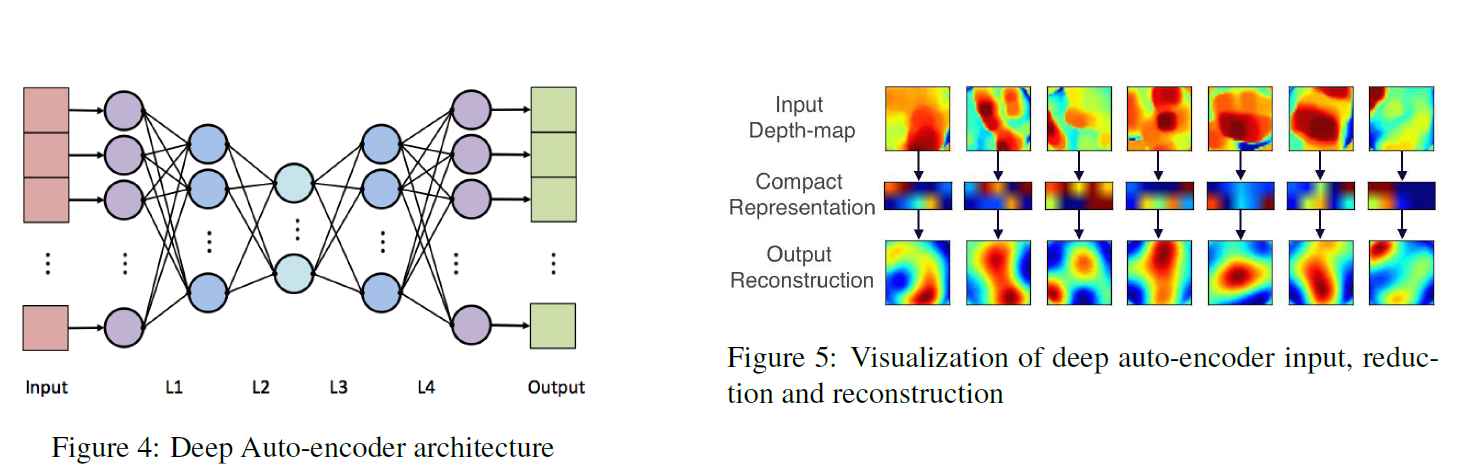
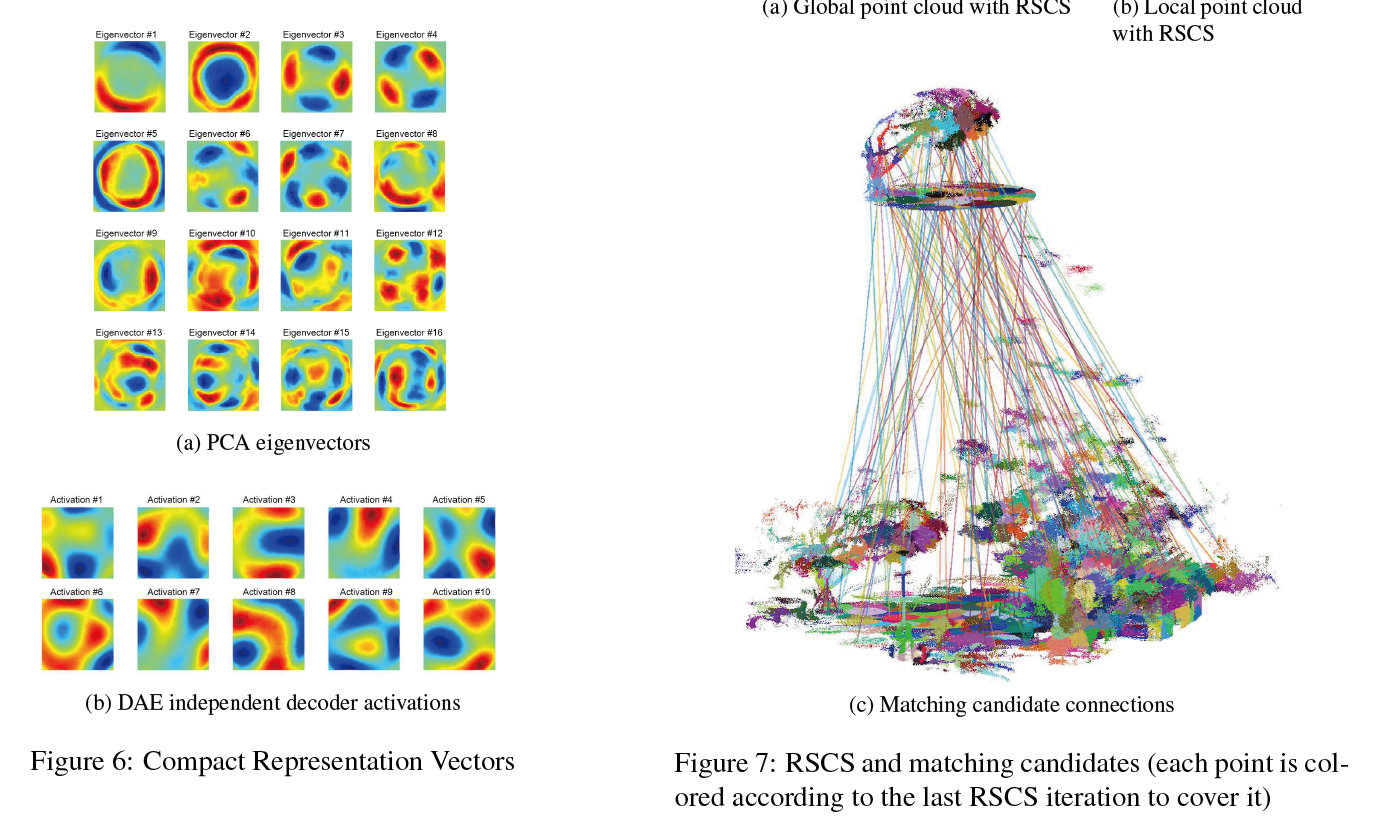
Deep Neural Network Auto-Encoder
| Repository | spark | star |
|---|---|---|
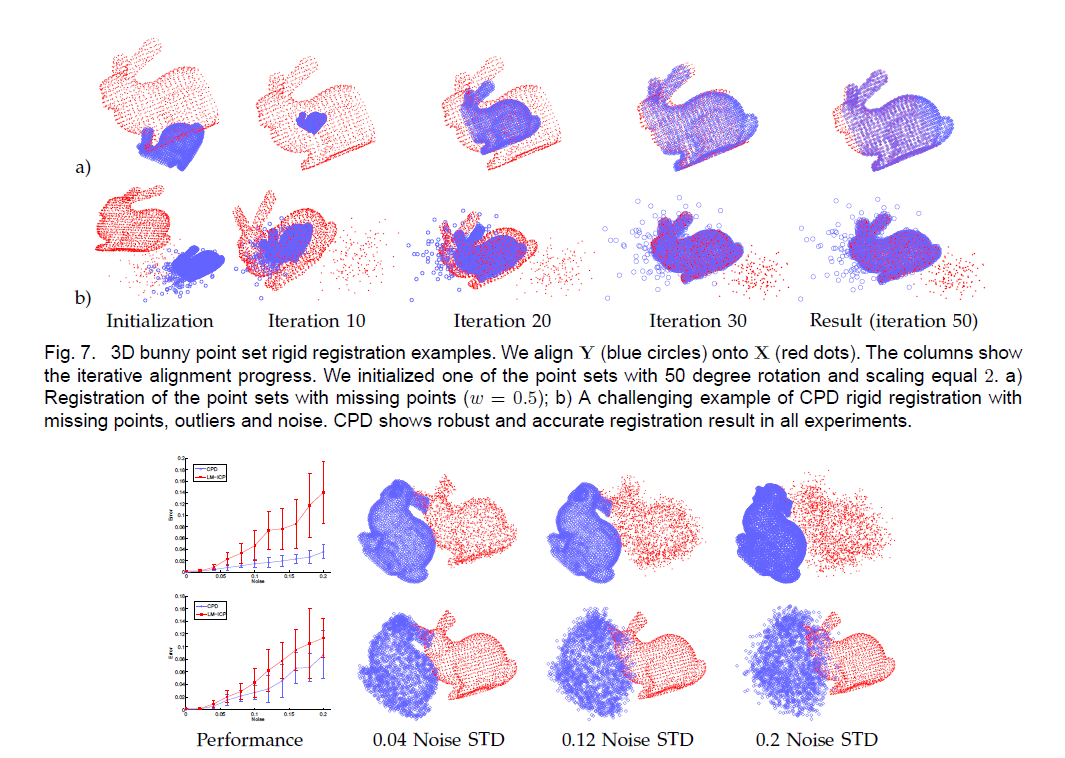
Coherent Point Drift
| Repository | spark | star |
|---|---|---|
变换层次
- 关于自由度
- 与泛函无关的不变量数等于或大于配置的自由度数减去变换的自由度数
2D
- 《Multiple View Geometry in Computer Vision》2.4.7