Operator For Image

Sobel Operator - 1968 [索伯算子, 索贝尔算子]

• Paper - An Isotropic 3x3 Image Gradient Operator
• Paper.pdf
• Formula
  • $$ \begin{aligned} G_x &= \begin{bmatrix} +1&0&-1\\+2&0&-2\\+1&0&-1\\ \end{bmatrix} * IMG\\ G_y &= \begin{bmatrix} +1&+2&+1\\0&0&0\\-1&-2&-1\\ \end{bmatrix} * IMG\\ G &= \sqrt{G_x^2 + G_y^2}\\ \Theta &= \arctan(\frac{G_y}{G_x})=atan2(G_x, G_y) \end{aligned} $$
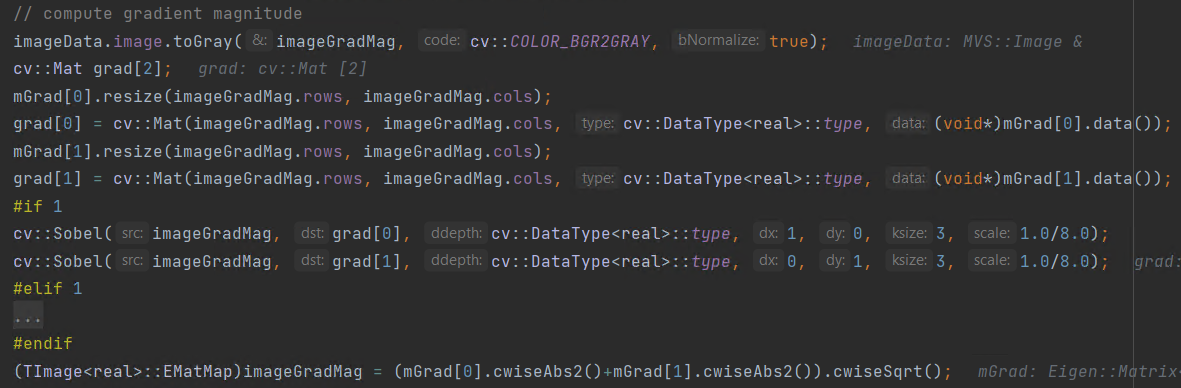
• OpenMvs
  • 
• Related
  • Digital step edges from zero crossing of second directional derivatives
  • Paper.pdf
  • 
• 
• 

Scharr Operator(Filter) - 2000 [沙尔算子]

• Paper written in German - Optimal operators in digital image processing
• 
• Paper.pdf

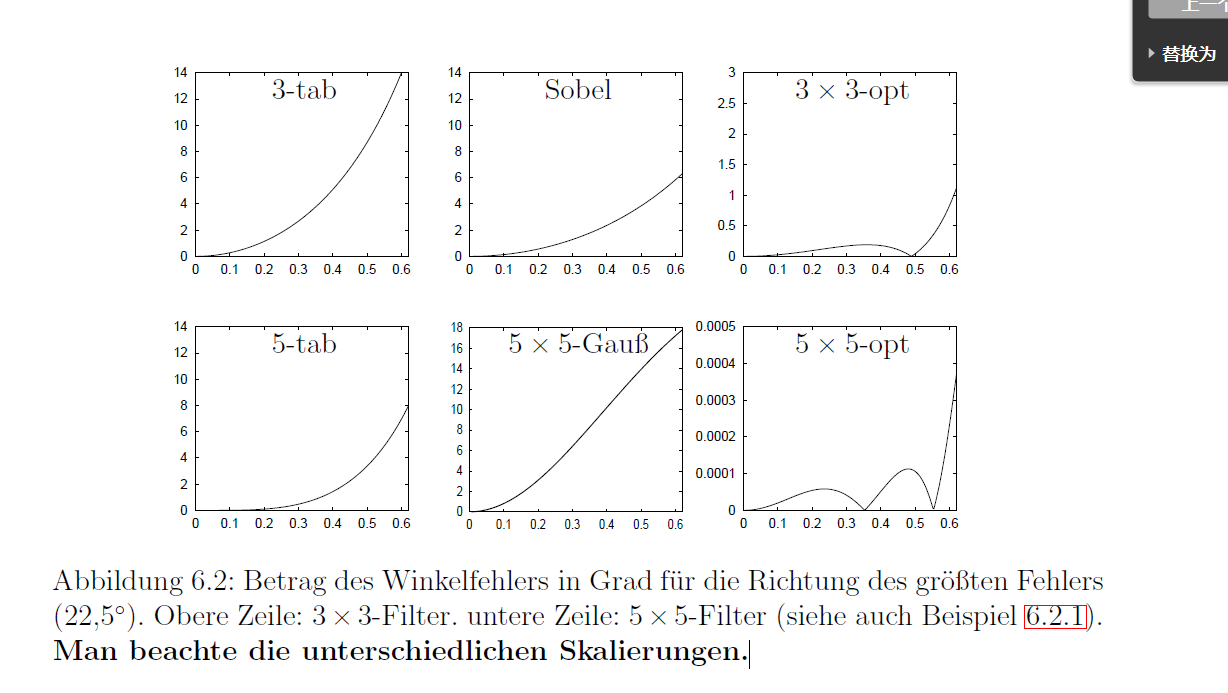
  • Sobel Operator does not exhibit a good rotational symmetry (about 1° of error)

  • The Scharr filter results in a less rotational variance than the Sobel filter scikit - edge filter

  • $$ \begin{aligned} \alpha_{1,ref}(\mathbf{\tilde{k}})&=\arctan(\frac{\tilde{k_y}}{\tilde{k_x}})\\ \alpha_{1}(\mathbf{\tilde{k},d})&=\arctan(\frac{\hat{D}_y}{\hat{D}_x})\\ d(\mathbf{\tilde{k,d}})&=\alpha_{1}(\mathbf{\tilde{k},d}) - \alpha_{1,ref}(\mathbf{\tilde{k}}) \end{aligned} $$
  • 
• Formula
  • $$ \begin{aligned} G_x &= \begin{bmatrix} +3&0&-3\\+10&0&-10\\+3&0&-3\\ \end{bmatrix} * IMG\\ G_y &= \begin{bmatrix} +3&+10&+3\\0&0&0\\-3&-10&-3\\ \end{bmatrix} * IMG\\ G &= \sqrt{G_x^2 + G_y^2}\\ \Theta &= \arctan(\frac{G_y}{G_x})=atan2(G_x, G_y) \end{aligned} $$
• 
• 

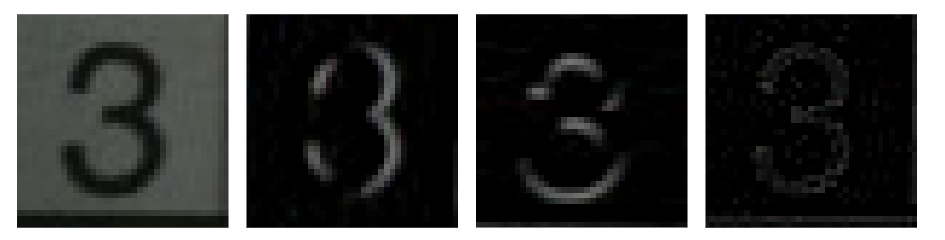
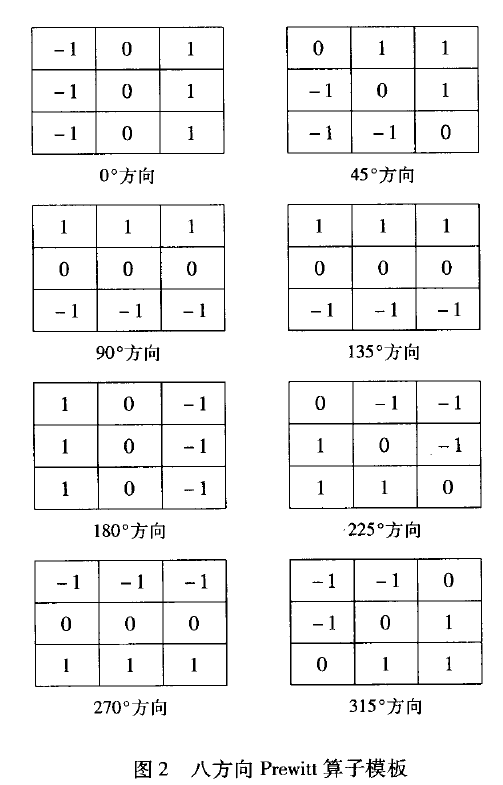
Prewitt operator - 1970 [普鲁伊特算子]

• Book - Object Enhancement and Extraction
• 
• Formula
  • $$ \begin{aligned} G_x &= \begin{bmatrix} +1&0&-1\\+1&0&-1\\+1&0&-1\\ \end{bmatrix} * IMG\\ G_y &= \begin{bmatrix} +1&+1&+1\\0&0&0\\-1&-1&-1\\ \end{bmatrix} * IMG\\ G &= \sqrt{G_x^2 + G_y^2}\\ \Theta &= \arctan(\frac{G_y}{G_x})=atan2(G_x, G_y) \end{aligned} $$
• Related
  • 一种改进的图像边缘检测算法💩🤮
  • 
  • Paper.pdf
  • 

Roberts cross [罗伯茨算子]

• Machine Perception Of Three-Dimensional Solids
• 
• Formula
  • $$ \begin{aligned} G_x &= \begin{bmatrix} +1&0\\0&-1 \end{bmatrix} * IMG\\ G_y &= \begin{bmatrix} 0&+1\\-1&0 \end{bmatrix} * IMG\\ G &= \sqrt{G_x^2 + G_y^2}\\ \Theta &= \arctan(\frac{G_y}{G_x})-\frac{3\pi}{4} \end{aligned} $$

Compare of them