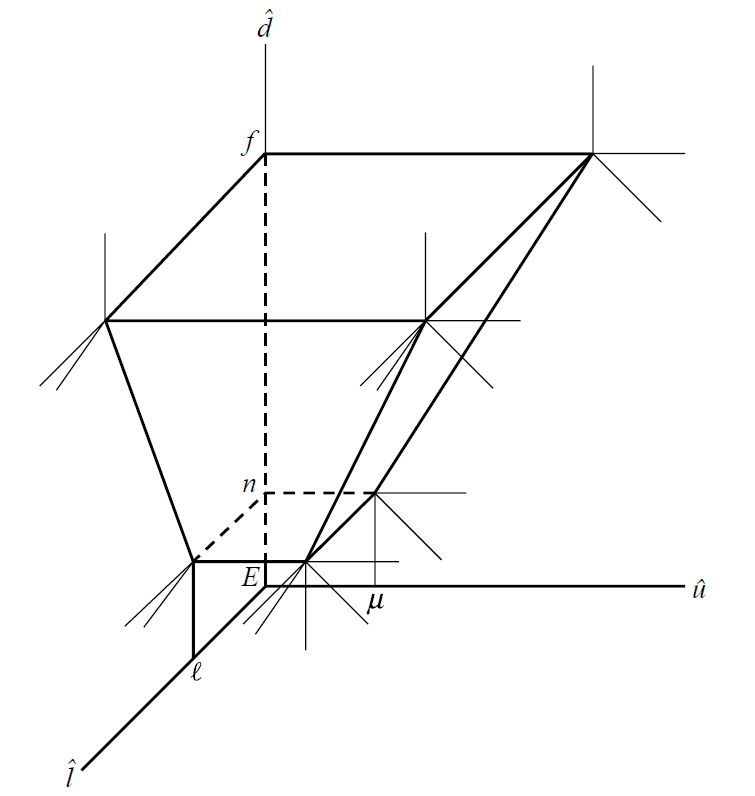
Minimum bounding box [MBB]
MBB 最小包围盒 [Minimum bounding box]
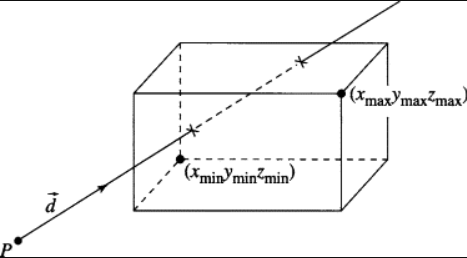
AABB 轴对齐包围盒 [Axis-aligned minimum bounding box]
-
when the model is rotated they cannot be simply rotated with it, but need to be recomputed.
-
-
$$ \begin{aligned} P_{min} &= [x_{min},y_{min},z_{min}]\\ P_{max} &= [x_{max},y_{max},z_{max}] \end{aligned} $$
OBB 有向围盒 [Oriented minimum bounding box]
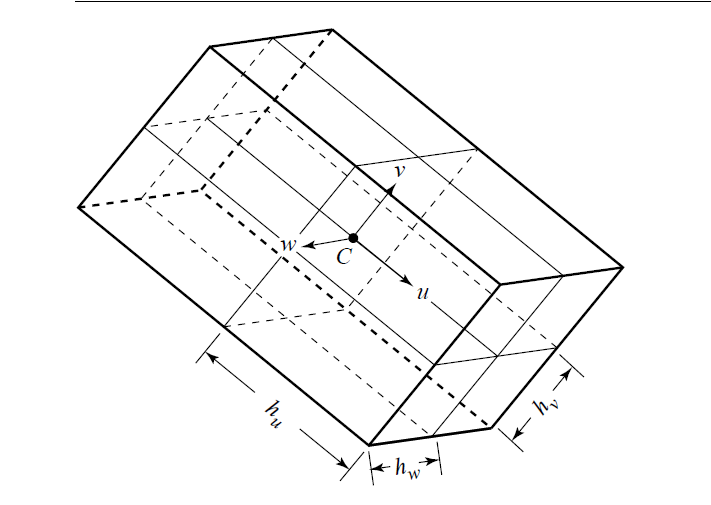
- 其中
- $C$: Center Point
- $\mathbf{u, v, w}$: three unit vectors orthornormal basis
- $h_u, h_v, h_w$: three scalars representing half the dimension in each directions
- Arbitrarily oriented minimum bounding box
- Object-oriented minimum bounding box
DOP 离散定向多面体 [Discrete Oriented Polyhedra]
-
A k-DOP is the Boolean intersection of extents along k directions. Thus, a k-DOP is the Boolean intersection of k bounding slabs and is a convex polytope containing the object
Intersection checks
Oriented Bounding Box and Orthogonal Frustum [OBB 和 方平截头体, 正交平截头体]
- Orthogonal Frustum, usually is the viewing frustum[视体]
- The Method of Separating Axes [分离轴定理]
- Hyperplane separation theorem - Wikipidea
- Separating Axis Theorem (SAT) Explanation
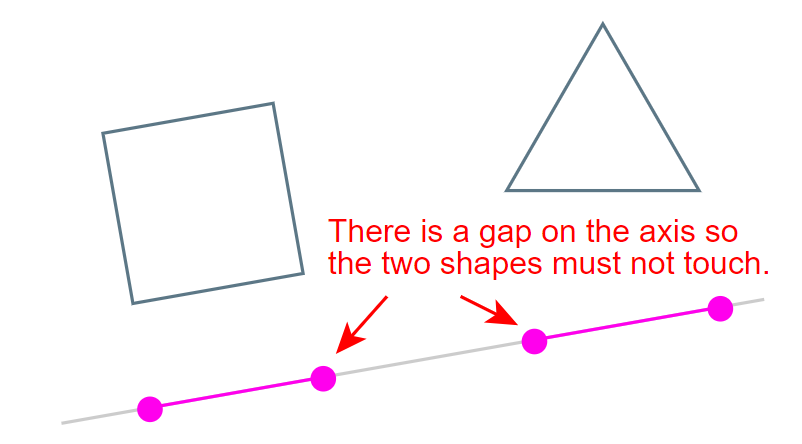
- 取一条边,做每个点在其法向上的投影,对每个形状取最大值和最小值作为投影范围,判断投影是否相交即可,如果投影不想交,则两个图形必然不想交,否则继续迭代下一个边,如果所有的边都相交,则物体相交
- 本方法只适用于凸多面体
-
difficult problem is selecting a finite set of line directions such that the intersection/nonintersection can be determined by separating axis tests using only vectors in that set
- 减少需要迭代的边可以提高运行速度
-
For convex polyhedra it turns out that the set consisting of face normals for the two polyhedra and vectors that are the cross product of edges, one edge from each polyhedron, is sufficient for the intersection testing.
- 对于一个多面体$i$,有$F_i, E_i$个面和边,需要检测的直线总量为$F_0+F_1+E_0E_1$
-
It is possible that some of the vectors formed by cross products of edges are zero, in which case they do not need to be tested
- For
OBBandOF- OBB: $F=3, E=3$
- OF: $F=5, E=6$
- The total number of vectors to test is $26$
- Caching Intermediate Results to make an optimized implementation
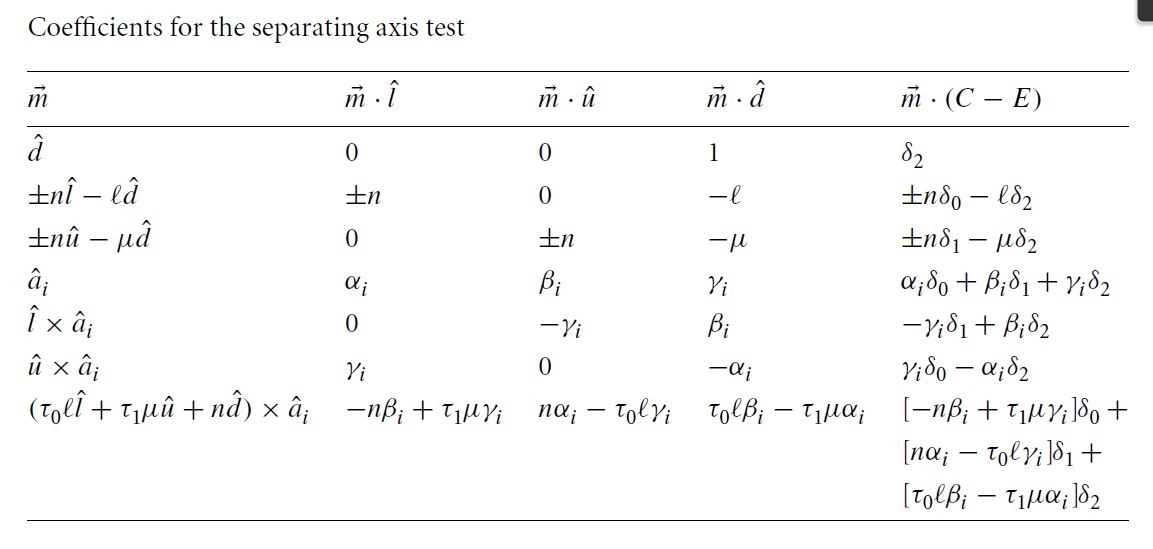
- For
AABBandAABB- AABB: $F=3, E=3$
- The total number of vectors to test is $3+3+3*3=15$
- The set has only three nonzero vectors.
- For
OBBandOBB- OBB: $F=3, E=3$
- Total: $3 + 3+ 3*3=15$
- For
平面与包围盒的相交测试
- 对角线判定法
- 利用了平面与包围盒相交,则它必定与包围盒的一条对角线相交这个性质,所以只要找到那条对角线,把它的两个顶点代入平面的方程中,判断求解的结果的符号即可
- 距离判定法
- 是通过对比投影半长与包围盒中心到平面的距离来判定是否相交
射线与包围盒的相交测试
OpenMVS[距离判定法?]
/**
* Culls AABB to n sided frustum. Normals pointing outwards.
* -> IN: AABB - bounding box to be tested
* OUT: VISIBLE - aabb totally inside frustum
* CLIPPED - aabb clipped by frustum
* CULLED - aabb totally outside frustum
*/
GCLASS TFrustum<TYPE,DIMS>::Classify(const AABB& aabb) const
{
bool bIntersects = false;
// find and test extreme points
for (int i=0; i<DIMS; ++i) {
const PLANE& plane = m_planes[i];
POINT ptPlaneMin, ptPlaneMax;
// x coordinate
if (plane.m_vN(0) >= TYPE(0)) {
ptPlaneMin(0) = aabb.ptMin(0);
ptPlaneMax(0) = aabb.ptMax(0);
} else {
ptPlaneMin(0) = aabb.ptMax(0);
ptPlaneMax(0) = aabb.ptMin(0);
}
// y coordinate
if (plane.m_vN(1) >= TYPE(0)) {
ptPlaneMin(1) = aabb.ptMin(1);
ptPlaneMax(1) = aabb.ptMax(1);
} else {
ptPlaneMin(1) = aabb.ptMax(1);
ptPlaneMax(1) = aabb.ptMin(1);
}
// z coordinate
if (plane.m_vN(2) >= TYPE(0)) {
ptPlaneMin(2) = aabb.ptMin(2);
ptPlaneMax(2) = aabb.ptMax(2);
} else {
ptPlaneMin(2) = aabb.ptMax(2);
ptPlaneMax(2) = aabb.ptMin(2);
}
if (plane.m_vN.dot(ptPlaneMin) > -plane.m_fD)
return CULLED;
if (plane.m_vN.dot(ptPlaneMax) >= -plane.m_fD)
bIntersects = true;
} // for
if (bIntersects) return CLIPPED;
return VISIBLE;
}