Inpainting

Loss

• pixel loss
  • $\mathcal{L}=|I_{est}-I_{HR}|_2^2$
  • $I_{est}$估计图像，$I_{HR}$高清图像
• perceptual loss
  • $\mathcal{L}=|\phi(I_{est})-\phi(I_{HR})|_2^2$
  • $\phi(*)$ VGG-19的第二和第五pooling层
• texture matching loss
  • $\mathcal{L}=|G(\phi(I_{est}))-G(\phi(I_{HR}))|_2^2$
  • $G(F)=F·F^T$, 为Gram矩阵
• Adversarial loss
  • G 最小化loss
    • $\mathcal{L}=-log(D(G(z)))$
  • D 最小化
    • $\mathcal{L}=-log(D(x))-log(1-D(G(z)))$
• Content Loss 内容损失
  • 讲解^[DeepLearning.ai学习笔记（四）卷积神经网络 – week4 特殊应用:人力脸识别和神经风格转换]
  • 讲解CSDN^[神经网络风格迁移Pytorch]
  • $\mathcal{L}_{content}^{l}=\frac{1}{2}|A^{l}(C)-A^{l}(G)|^2$
  • $l$为层数，通常取vgg中间层，浅层为像素级别，深层为语义级别
  • $C$内容图像
  • $G$风格图像
  • $A$为激活层
• Style loss 风格损失
  • $\mathcal{L}{Style}^{l}=\frac{1}{(2n_H^{l}n_W^{l}n_C^{l})^2}\sum{k}\sum_{k’}(Gram_{kk’}^{l}(S)-Gram_{kk’}^{l}(G))$
  • $l$为层数
  • $Gram$为$Gram$矩阵$G_{kk’}^{l}(S)=\sum_{i=1}^{n_H^{l}}\sum_{j=1}^{n_W^{l}}A_{i,j,k}^{l}(S)A_{i,j,k’}^{l}(S)$
    • $Gram$ $size=(n_c^l,n_c^l)$
  • $n_H^{l}$为第l层的H大小
  • $\mathcal{L}{style}(S, G)=\sum_l\lambda^l\mathcal{L}{style}^l(S,G)$
• PAN^[Perceptual Adversarial Networks:TIP 2018]
  • 
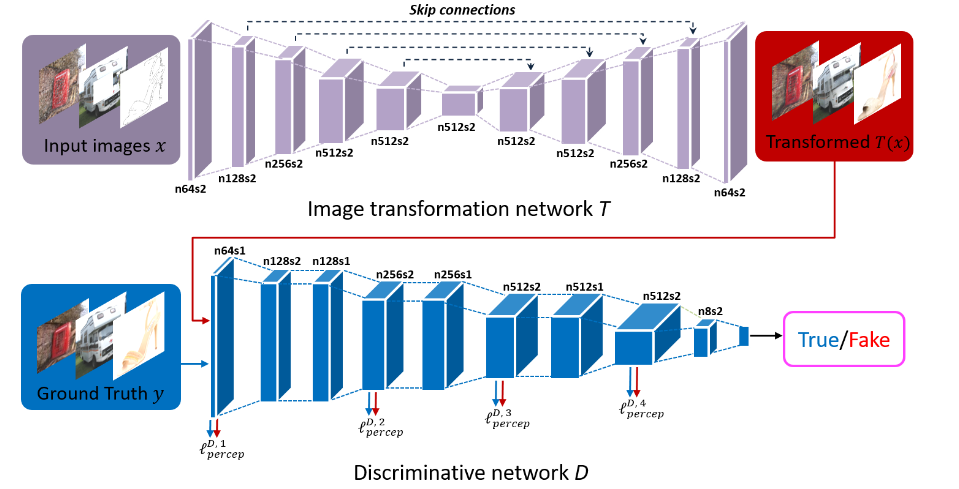
  • $\mathcal{l}_{percep}^{D,j}(x,y)=|D_j(y)-D_j(T(x))|$
  • $\mathcal{L}T=\sum{j=1}^F\lambda_j\mathcal{l}_{percep}^{D,j}$

• GAN

• $\underset{G}{\min}\ \underset{D}{\max}(D,G)=E_{x\sim p_{data}(x)}[logD(x)]+E_{z\sim p_{z}}[log(1-D(G(z)))]$
  • $D$ 判别网络 Discriminant
  • $G$ 生成网络
  • 寻找最优的判别网络可以区分生成的和真实的图片的区别
  • 寻找最优的生成网络，避免被判别网络判别

Paper

• Feature Learning by Inpainting^[Context Encoders: Feature Learning by Inpainting: cvpr 2016]
  • GAN, 论文中有random mask, 代码中只有center cropped
  • 对mask区域的训练，是将图像mask部分设置为灰色，训练时并未区分与其他位置的差异
  • 对mask区域pixel的损失计算，增加了一些权重，使得mask和非mask区域区分开来
• CR-Fill^[Generative Image Inpainting with Auxiliary Contexutal Reconstruction ICCV 2021]
  • 随机mask
  • $\mathcal{L}D=\mathbb{E}{X\sim p_{data}(X)}\big[ReLU(1-D(X))\big]+\mathbb{E}{X\sim p{U}(U)}\big[ReLU(1-D(G(U)\circ M+U))\big]$
    • $X$ ground-trutu
    • $U$ incomplete image with the pixels in the missing regions set to zero
    • $M$ binary mask, 1: missing, 0 known
    • $G(·)$ generator
• Partial Convolutions^[Image Inpainting for Irregular Holes Using Partial Convolutions TOG 2017]^[Partial Convolutions Official Implementation]
  • 
  • $x’=\begin{cases}W^T(X\bigodot M)\frac{1}{M} + b&, if sum(M)>0\0&,other